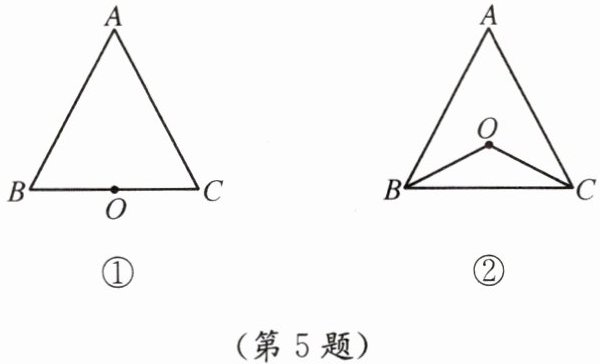
5. 如图,在△ABC中,已知点O到边AB,AC的距离分别是OD,OE,且OD= OE,OB= OC.
(1) 如图①,若点O在边BC上,补全图形并证明AB= AC;
(2) 如图②,若点O在△ABC的内部,补全图形并证明AB= AC.
(1) 如图①,若点O在边BC上,补全图形并证明AB= AC;
(2) 如图②,若点O在△ABC的内部,补全图形并证明AB= AC.

答案:(1) 补全图形:过点O作OD⊥AB于D,OE⊥AC于E。
证明:∵OD⊥AB,OE⊥AC,∴∠ODB=∠OEC=90°。
在Rt△ODB和Rt△OEC中,OB=OC,OD=OE,∴Rt△ODB≌Rt△OEC(HL)。
∴∠B=∠C,∴AB=AC。
(2) 补全图形:过点O作OD⊥AB于D,OE⊥AC于E。
证明:∵OD⊥AB,OE⊥AC,∴∠ODB=∠OEC=90°。
在Rt△ODB和Rt△OEC中,OB=OC,OD=OE,∴Rt△ODB≌Rt△OEC(HL)。
∴∠OBD=∠OCE。
∵OB=OC,∴∠OBC=∠OCB。
∴∠OBD+∠OBC=∠OCE+∠OCB,即∠ABC=∠ACB。
∴AB=AC。
证明:∵OD⊥AB,OE⊥AC,∴∠ODB=∠OEC=90°。
在Rt△ODB和Rt△OEC中,OB=OC,OD=OE,∴Rt△ODB≌Rt△OEC(HL)。
∴∠B=∠C,∴AB=AC。
(2) 补全图形:过点O作OD⊥AB于D,OE⊥AC于E。
证明:∵OD⊥AB,OE⊥AC,∴∠ODB=∠OEC=90°。
在Rt△ODB和Rt△OEC中,OB=OC,OD=OE,∴Rt△ODB≌Rt△OEC(HL)。
∴∠OBD=∠OCE。
∵OB=OC,∴∠OBC=∠OCB。
∴∠OBD+∠OBC=∠OCE+∠OCB,即∠ABC=∠ACB。
∴AB=AC。
6. 如图,在△ABC和△A'B'C'中,AC= A'C',BC= B'C',∠B= ∠B',且∠B,∠B'都是钝角.求证:△ABC≌△A'B'C'.


答案:证明:分别过点C、C'作CD⊥AB交AB延长线于点D,C'D'⊥A'B'交A'B'延长线于点D'。
∵∠ABC、∠A'B'C'是钝角,
∴点D在AB延长线上,点D'在A'B'延长线上。
∴∠CBD=180°-∠ABC,∠C'B'D'=180°-∠A'B'C'。
∵∠ABC=∠A'B'C',
∴∠CBD=∠C'B'D'。
在△CBD和△C'B'D'中,
∠CDB=∠C'D'B'=90°,
∠CBD=∠C'B'D',
BC=B'C',
∴△CBD≌△C'B'D'(AAS)。
∴CD=C'D',BD=B'D'。
在Rt△ACD和Rt△A'C'D'中,
AC=A'C',
CD=C'D',
∴Rt△ACD≌Rt△A'C'D'(HL)。
∴AD=A'D'。
∵AD=AB+BD,A'D'=A'B'+B'D',BD=B'D',
∴AB=A'B'。
在△ABC和△A'B'C'中,
AB=A'B',
∠ABC=∠A'B'C',
BC=B'C',
∴△ABC≌△A'B'C'(SAS)。
∵∠ABC、∠A'B'C'是钝角,
∴点D在AB延长线上,点D'在A'B'延长线上。
∴∠CBD=180°-∠ABC,∠C'B'D'=180°-∠A'B'C'。
∵∠ABC=∠A'B'C',
∴∠CBD=∠C'B'D'。
在△CBD和△C'B'D'中,
∠CDB=∠C'D'B'=90°,
∠CBD=∠C'B'D',
BC=B'C',
∴△CBD≌△C'B'D'(AAS)。
∴CD=C'D',BD=B'D'。
在Rt△ACD和Rt△A'C'D'中,
AC=A'C',
CD=C'D',
∴Rt△ACD≌Rt△A'C'D'(HL)。
∴AD=A'D'。
∵AD=AB+BD,A'D'=A'B'+B'D',BD=B'D',
∴AB=A'B'。
在△ABC和△A'B'C'中,
AB=A'B',
∠ABC=∠A'B'C',
BC=B'C',
∴△ABC≌△A'B'C'(SAS)。