如果一个数有算术平方根,那么这个数一定有平方根吗?有几个?负数为什么没有平方根?
答案:【解析】:
本题主要考查平方根和算术平方根的概念及其性质。
首先,我们需要明确什么是算术平方根和平方根。
算术平方根:若一个非负数$x$的平方等于$a$,即$x^2 = a$,则这个数$x$被称为$a$的算术平方根。
平方根:若一个数$x$的平方等于$a$,即$x^2 = a$,则这个数$x$被称为$a$的平方根。
根据定义,我们可以得出以下结论:
如果一个数有算术平方根,那么这个数一定是非负数,因为负数没有算术平方根。
由于非负数包括0和正数,而0和正数都有平方根(0的平方根是0,正数的平方根有两个,一个正数和一个负数),所以这个数一定有平方根,且至少有一个(0的情况)或两个(正数的情况)。
负数没有平方根,因为在实数范围内,没有任何数的平方是负数。
【答案】:
如果一个数有算术平方根,那么这个数一定有平方根。这个数可能是0或正数。0有一个平方根(即0本身),正数有两个平方根(一个正数和一个负数)。负数没有平方根,因为在实数范围内,没有任何数的平方是负数。
本题主要考查平方根和算术平方根的概念及其性质。
首先,我们需要明确什么是算术平方根和平方根。
算术平方根:若一个非负数$x$的平方等于$a$,即$x^2 = a$,则这个数$x$被称为$a$的算术平方根。
平方根:若一个数$x$的平方等于$a$,即$x^2 = a$,则这个数$x$被称为$a$的平方根。
根据定义,我们可以得出以下结论:
如果一个数有算术平方根,那么这个数一定是非负数,因为负数没有算术平方根。
由于非负数包括0和正数,而0和正数都有平方根(0的平方根是0,正数的平方根有两个,一个正数和一个负数),所以这个数一定有平方根,且至少有一个(0的情况)或两个(正数的情况)。
负数没有平方根,因为在实数范围内,没有任何数的平方是负数。
【答案】:
如果一个数有算术平方根,那么这个数一定有平方根。这个数可能是0或正数。0有一个平方根(即0本身),正数有两个平方根(一个正数和一个负数)。负数没有平方根,因为在实数范围内,没有任何数的平方是负数。
例1 求下列各数的平方根:
(1)10 000;
(2)$\frac{9}{16}$;
(3)0.25;
(4)$10^{6}$.
(1)10 000;
(2)$\frac{9}{16}$;
(3)0.25;
(4)$10^{6}$.
答案:解:(1)因为$ (\pm 100)^{2}=10000 $,所以10000的平方根是$ \pm 100 $。
(2)因为$ (\pm \frac{3}{4})^{2}=\frac{9}{16} $,所以$ \frac{9}{16} $的平方根是$ \pm \frac{3}{4} $。
(3)因为$ (\pm 0.5)^{2}=0.25 $,所以0.25的平方根是$ \pm 0.5 $。
(4)因为$ (\pm 10^{3})^{2}=10^{6} $,所以$ 10^{6} $的平方根是$ \pm 1000 $。
(2)因为$ (\pm \frac{3}{4})^{2}=\frac{9}{16} $,所以$ \frac{9}{16} $的平方根是$ \pm \frac{3}{4} $。
(3)因为$ (\pm 0.5)^{2}=0.25 $,所以0.25的平方根是$ \pm 0.5 $。
(4)因为$ (\pm 10^{3})^{2}=10^{6} $,所以$ 10^{6} $的平方根是$ \pm 1000 $。
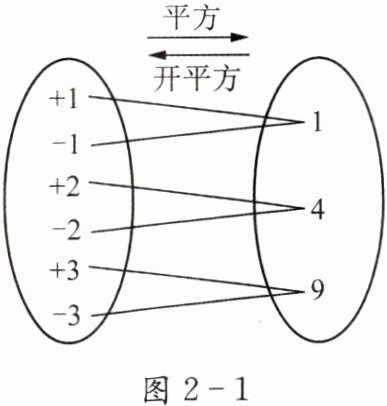
例2 观察并仿照图2-1,画出一个类似的图形,并写出一条正确的结论.

答案:解:
(图形绘制:左侧椭圆内写+4、-4、+5、-5;右侧椭圆内写16、25;左侧+4、-4分别与右侧16用直线连接,左侧+5、-5分别与右侧25用直线连接,两椭圆间上方标“平方”箭头向右,下方标“开平方”箭头向左)
结论:一个正数有两个平方根,它们互为相反数。
(图形绘制:左侧椭圆内写+4、-4、+5、-5;右侧椭圆内写16、25;左侧+4、-4分别与右侧16用直线连接,左侧+5、-5分别与右侧25用直线连接,两椭圆间上方标“平方”箭头向右,下方标“开平方”箭头向左)
结论:一个正数有两个平方根,它们互为相反数。
1. 填空题:
(1)已知$x^{2}= 5$,那么x叫作5的
(2)因为$3^{2}= $
(3)正数的平方根有
(4)如果$x^{2}= 4^{2}$,那么$x= $
(1)已知$x^{2}= 5$,那么x叫作5的
平方根
,记作$\pm \sqrt{5}$
;(2)因为$3^{2}= $
9
,$(-3)^{2}= $9
,所以3和-3都是9
的平方根;(3)正数的平方根有
2
个,它们互为相反数
,0的平方根为0
,负数
没有平方根;(4)如果$x^{2}= 4^{2}$,那么$x= $
$\pm 4$
.答案:【解析】:
本题主要考查了平方根的定义及性质。
(1) 根据平方根的定义,若一个数的平方等于另一个数,则这个数是另一个数的平方根。
因此,当$x^{2} = 5$时,x是5的平方根,记作$\pm \sqrt{5}$。
(2) 根据平方的定义,$3^{2} = 9$,$(-3)^{2} = 9$。
因此,3和-3都是9的平方根。
(3) 正数的平方根有两个,一个正数和一个负数,它们互为相反数。
0的平方根是0本身,而负数没有平方根,因为任何实数的平方都是非负的。
(4) 根据平方根的性质,如果$x^{2} = a^{2}$,那么$x = \pm a$。
所以,当$x^{2} = 4^{2}$时,$x = \pm 4$。
【答案】:
(1) 平方根;$\pm \sqrt{5}$
(2) 9;9;9
(3) 2;相反数;0;负数
(4) $\pm 4$
本题主要考查了平方根的定义及性质。
(1) 根据平方根的定义,若一个数的平方等于另一个数,则这个数是另一个数的平方根。
因此,当$x^{2} = 5$时,x是5的平方根,记作$\pm \sqrt{5}$。
(2) 根据平方的定义,$3^{2} = 9$,$(-3)^{2} = 9$。
因此,3和-3都是9的平方根。
(3) 正数的平方根有两个,一个正数和一个负数,它们互为相反数。
0的平方根是0本身,而负数没有平方根,因为任何实数的平方都是非负的。
(4) 根据平方根的性质,如果$x^{2} = a^{2}$,那么$x = \pm a$。
所以,当$x^{2} = 4^{2}$时,$x = \pm 4$。
【答案】:
(1) 平方根;$\pm \sqrt{5}$
(2) 9;9;9
(3) 2;相反数;0;负数
(4) $\pm 4$
2. 选择题:
(1)9的平方根是±3,用数学符号表示,正确的是(
A. $\sqrt{9}= 3$
B. $\pm\sqrt{9}= 3$
C. $\sqrt{9}= \pm3$
D. $\pm\sqrt{9}= \pm3$
(2)下列说法中,正确的是(
A. 任何数的平方根都有两个
B. 一个正数的平方根的平方是它本身
C. 只有正数才有平方根
D. 正数的平方根是正数
(1)9的平方根是±3,用数学符号表示,正确的是(
D
).A. $\sqrt{9}= 3$
B. $\pm\sqrt{9}= 3$
C. $\sqrt{9}= \pm3$
D. $\pm\sqrt{9}= \pm3$
(2)下列说法中,正确的是(
B
).A. 任何数的平方根都有两个
B. 一个正数的平方根的平方是它本身
C. 只有正数才有平方根
D. 正数的平方根是正数
答案:【解析】:
本题考查了平方根的定义及其性质。对于第一题,我们需要理解平方根的表示方法,特别是正负平方根的表示;对于第二题,我们需要根据平方根的性质,逐一判断每个选项的正确性。
(1)
A选项:$\sqrt{9}= 3$,这表示9的正平方根是3,但题目要求的是9的平方根包括正负两个值,所以A选项错误。
B选项:$\pm\sqrt{9}= 3$,这表示9的平方根的正负值都等于3,这是不可能的,因为$-\sqrt{9} = -3$,所以B选项错误。
C选项:$\sqrt{9}= \pm3$,这表示9的平方根既可以是3也可以是-3,但数学符号上,$\sqrt{9}$通常只表示正平方根,所以C选项错误。
D选项:$\pm\sqrt{9}= \pm3$,这正确地表示了9的平方根包括正负两个值,所以D选项正确。
(2)
A选项:任何数的平方根都有两个,这是不正确的。例如,0的平方根只有一个,即0本身;负数没有实数平方根。所以A选项错误。
B选项:一个正数的平方根的平方是它本身,这是正确的。设正数为a,其平方根为$\sqrt{a}$和$-\sqrt{a}$,它们的平方都是a。所以B选项正确。
C选项:只有正数才有平方根,这是不正确的。0也有平方根,即0本身。所以C选项错误。
D选项:正数的平方根是正数,这是不正确的。正数的平方根有两个,一个正数和一个负数。所以D选项错误。
【答案】:
(1) D
(2) B
本题考查了平方根的定义及其性质。对于第一题,我们需要理解平方根的表示方法,特别是正负平方根的表示;对于第二题,我们需要根据平方根的性质,逐一判断每个选项的正确性。
(1)
A选项:$\sqrt{9}= 3$,这表示9的正平方根是3,但题目要求的是9的平方根包括正负两个值,所以A选项错误。
B选项:$\pm\sqrt{9}= 3$,这表示9的平方根的正负值都等于3,这是不可能的,因为$-\sqrt{9} = -3$,所以B选项错误。
C选项:$\sqrt{9}= \pm3$,这表示9的平方根既可以是3也可以是-3,但数学符号上,$\sqrt{9}$通常只表示正平方根,所以C选项错误。
D选项:$\pm\sqrt{9}= \pm3$,这正确地表示了9的平方根包括正负两个值,所以D选项正确。
(2)
A选项:任何数的平方根都有两个,这是不正确的。例如,0的平方根只有一个,即0本身;负数没有实数平方根。所以A选项错误。
B选项:一个正数的平方根的平方是它本身,这是正确的。设正数为a,其平方根为$\sqrt{a}$和$-\sqrt{a}$,它们的平方都是a。所以B选项正确。
C选项:只有正数才有平方根,这是不正确的。0也有平方根,即0本身。所以C选项错误。
D选项:正数的平方根是正数,这是不正确的。正数的平方根有两个,一个正数和一个负数。所以D选项错误。
【答案】:
(1) D
(2) B