例1 下列各数中,哪些是有理数?哪些是无理数?
$\sqrt{289}$,$\frac{1}{2}$,$\sqrt{5}$,$\frac{22}{7}$,0.2020020002…(相邻的两个2之间依次多一个0),$\sqrt[3]{-27}$,$\frac{\pi}{3}$,$-0.\dot{8}\dot{9}$,$\sqrt[3]{9}$.
$\sqrt{289}$,$\frac{1}{2}$,$\sqrt{5}$,$\frac{22}{7}$,0.2020020002…(相邻的两个2之间依次多一个0),$\sqrt[3]{-27}$,$\frac{\pi}{3}$,$-0.\dot{8}\dot{9}$,$\sqrt[3]{9}$.
答案:【解析】:
本题主要考察有理数和无理数的定义及判断。
有理数是可以表示为两个整数的比的数,包括整数、有限小数和循环小数。
无理数则不能表示为两个整数的比,常见的无理数有开方后不是整数的数值、π、e等。
根据这些定义,我们可以逐一判断给出的数:
$\sqrt{289}$:289是17的平方,所以$\sqrt{289}=17$,是有理数。
$\frac{1}{2}$:是两个整数的比,是有理数。
$\sqrt{5}$:5的平方根不能表示为两个整数的比,是无理数。
$\frac{22}{7}$:是两个整数的比,是有理数。
$0.2020020002\ldots$(相邻的两个2之间依次多一个0):是无限不循环小数,是无理数。
$\sqrt[3]{-27}$:-27的立方根是-3,是有理数。
$\frac{\pi}{3}$:π是无理数,所以$\frac{\pi}{3}$也是无理数。
$-0.\dot{8}\dot{9}$:是循环小数,是有理数。
$\sqrt[3]{9}$:9的立方根不能表示为两个整数的比,是无理数。
【答案】:
有理数:$\sqrt{289}$,$\frac{1}{2}$,$\frac{22}{7}$,$\sqrt[3]{-27}$,$-0.\dot{8}\dot{9}$;
无理数:$\sqrt{5}$,$0.2020020002\ldots$(相邻的两个2之间依次多一个0),$\frac{\pi}{3}$,$\sqrt[3]{9}$。
本题主要考察有理数和无理数的定义及判断。
有理数是可以表示为两个整数的比的数,包括整数、有限小数和循环小数。
无理数则不能表示为两个整数的比,常见的无理数有开方后不是整数的数值、π、e等。
根据这些定义,我们可以逐一判断给出的数:
$\sqrt{289}$:289是17的平方,所以$\sqrt{289}=17$,是有理数。
$\frac{1}{2}$:是两个整数的比,是有理数。
$\sqrt{5}$:5的平方根不能表示为两个整数的比,是无理数。
$\frac{22}{7}$:是两个整数的比,是有理数。
$0.2020020002\ldots$(相邻的两个2之间依次多一个0):是无限不循环小数,是无理数。
$\sqrt[3]{-27}$:-27的立方根是-3,是有理数。
$\frac{\pi}{3}$:π是无理数,所以$\frac{\pi}{3}$也是无理数。
$-0.\dot{8}\dot{9}$:是循环小数,是有理数。
$\sqrt[3]{9}$:9的立方根不能表示为两个整数的比,是无理数。
【答案】:
有理数:$\sqrt{289}$,$\frac{1}{2}$,$\frac{22}{7}$,$\sqrt[3]{-27}$,$-0.\dot{8}\dot{9}$;
无理数:$\sqrt{5}$,$0.2020020002\ldots$(相邻的两个2之间依次多一个0),$\frac{\pi}{3}$,$\sqrt[3]{9}$。
例2 找一个有理数a,使$-\sqrt{3}<a<-\sqrt{2}$.
答案:解:因为$\sqrt{2}\approx1.414$,$\sqrt{3}\approx1.732$,所以$-\sqrt{3}\approx-1.732$,$-\sqrt{2}\approx-1.414$。
在$-1.732$和$-1.414$之间的有理数有很多,例如$-1.5$。
故$a$可以为$-1.5$(答案不唯一)。
在$-1.732$和$-1.414$之间的有理数有很多,例如$-1.5$。
故$a$可以为$-1.5$(答案不唯一)。
1. 填空题:
(1)
(2)
(1)
有理数
和无理数
统称为实数;(2)
实数
与数轴上的点一一对应.答案:【解析】:
本题考查了实数的基本概念和实数与数轴的关系。
对于填空(1),需要明确实数的定义,实数包括有理数和无理数。
对于填空(2),需要理解实数与数轴的关系,即每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点也都对应一个实数。
【答案】:
(1)有理数;无理数
(2)实数
本题考查了实数的基本概念和实数与数轴的关系。
对于填空(1),需要明确实数的定义,实数包括有理数和无理数。
对于填空(2),需要理解实数与数轴的关系,即每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点也都对应一个实数。
【答案】:
(1)有理数;无理数
(2)实数
2. 判断题(正确的打“√”,错误的打“×”):
(1)实数包括正实数、0、负实数;(
(2)所有有理数都可以用数轴上的点表示,反过来,数轴上所有的点都表示有理数.(
(1)实数包括正实数、0、负实数;(
√
)(2)所有有理数都可以用数轴上的点表示,反过来,数轴上所有的点都表示有理数.(
×
)答案:【解析】:
本题考查实数的定义和性质以及实数与数轴的关系。
(1) 对于第一个判断题,实数确实包括正实数、0和负实数。这是实数的定义之一,所以第一个判断题是正确的。
(2) 对于第二个判断题,虽然所有的有理数都可以在数轴上找到对应的点,但数轴上的点并不都表示有理数。例如,π和$\sqrt{2}$等无理数也可以在数轴上找到对应的点。因此,第二个判断题是错误的。
【答案】:
(1) √
(2) ×
本题考查实数的定义和性质以及实数与数轴的关系。
(1) 对于第一个判断题,实数确实包括正实数、0和负实数。这是实数的定义之一,所以第一个判断题是正确的。
(2) 对于第二个判断题,虽然所有的有理数都可以在数轴上找到对应的点,但数轴上的点并不都表示有理数。例如,π和$\sqrt{2}$等无理数也可以在数轴上找到对应的点。因此,第二个判断题是错误的。
【答案】:
(1) √
(2) ×
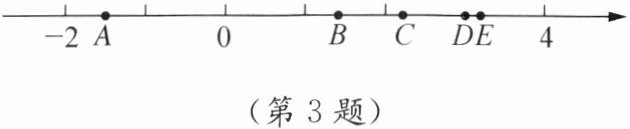
3. 将下列实数与图中数轴上标有字母的点对应起来.
$\sqrt{2}$,$-1.5$,$\sqrt{5}$,$\pi$,3
]
$\sqrt{2}$,$-1.5$,$\sqrt{5}$,$\pi$,3
]

答案:【解析】:
本题考查实数与数轴的关系,及实数在数轴上的位置判断,需要先判断各实数的大小,再与数轴上的点对应。
先分析已知的实数大小:
对于$\sqrt{2}$,因为$1^2 = 1$,$2^2 = 4$,且$1\lt 2\lt 4$,根据算术平方根的性质,可得$1\lt \sqrt{2}\lt 2$。
对于$-1.5$,它是一个负数,其值就是$-1.5$。
对于$\sqrt{5}$,由于$2^2 = 4$,$3^2 = 9$,且$4\lt 5\lt 9$,根据算术平方根的性质,可得$2\lt \sqrt{5}\lt 3$。
对于$\pi$,$\pi$是一个无限不循环小数,其近似值为$3.14$,所以$3\lt \pi\lt 4$。
数字$3$就是数轴上的$3$这个位置。
再与数轴上的点对应:
观察数轴可知,点$A$在$-2$和$0$之间且靠近$-2$,$-1.5$在$-2$和$0$之间且靠近$-2$的一半位置,所以$-1.5$与点$A$对应。
点$B$在$0$和$2$之间且靠近$0$,因为$1\lt \sqrt{2}\lt 2$,所以$\sqrt{2}$与点$B$对应。
点$C$在$2$和$3$之间,由于$2\lt \sqrt{5}\lt 3$,所以$\sqrt{5}$与点$C$对应。
点$D$在$3$和$4$之间且靠近$3$,因为$3\lt \pi\lt 4$,所以$\pi$与点$D$对应。
点$E$在$3$这个位置,所以$3$与点$E$对应。
【答案】:
$-1.5$与点$A$对应;$\sqrt{2}$与点$B$对应;$\sqrt{5}$与点$C$对应;$\pi$与点$D$对应;$3$与点$E$对应。
本题考查实数与数轴的关系,及实数在数轴上的位置判断,需要先判断各实数的大小,再与数轴上的点对应。
先分析已知的实数大小:
对于$\sqrt{2}$,因为$1^2 = 1$,$2^2 = 4$,且$1\lt 2\lt 4$,根据算术平方根的性质,可得$1\lt \sqrt{2}\lt 2$。
对于$-1.5$,它是一个负数,其值就是$-1.5$。
对于$\sqrt{5}$,由于$2^2 = 4$,$3^2 = 9$,且$4\lt 5\lt 9$,根据算术平方根的性质,可得$2\lt \sqrt{5}\lt 3$。
对于$\pi$,$\pi$是一个无限不循环小数,其近似值为$3.14$,所以$3\lt \pi\lt 4$。
数字$3$就是数轴上的$3$这个位置。
再与数轴上的点对应:
观察数轴可知,点$A$在$-2$和$0$之间且靠近$-2$,$-1.5$在$-2$和$0$之间且靠近$-2$的一半位置,所以$-1.5$与点$A$对应。
点$B$在$0$和$2$之间且靠近$0$,因为$1\lt \sqrt{2}\lt 2$,所以$\sqrt{2}$与点$B$对应。
点$C$在$2$和$3$之间,由于$2\lt \sqrt{5}\lt 3$,所以$\sqrt{5}$与点$C$对应。
点$D$在$3$和$4$之间且靠近$3$,因为$3\lt \pi\lt 4$,所以$\pi$与点$D$对应。
点$E$在$3$这个位置,所以$3$与点$E$对应。
【答案】:
$-1.5$与点$A$对应;$\sqrt{2}$与点$B$对应;$\sqrt{5}$与点$C$对应;$\pi$与点$D$对应;$3$与点$E$对应。