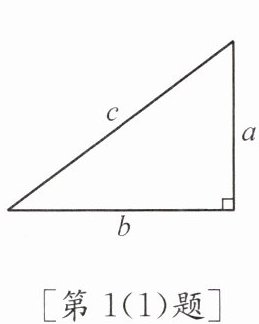
1.(1)直角三角形两条直角边长的平方和等于
(2)如图,图中数字与字母代表正方形的面积,那么$A= $

斜边的平方
,即直角三角形(如图)的两条直角边a,b与斜边c之间满足:$a^{2}+b^{2}=c^{2}$
.(2)如图,图中数字与字母代表正方形的面积,那么$A= $
25
,$B= $144
.

答案:1.(1)斜边的平方;$a^{2}+b^{2}=c^{2}$
(2)25;144
(2)25;144
2. 求图中直角三角形未知边的长度(阴影部分中的数字表示该阴影部分的面积).


答案:解:
第一个直角三角形:
∵两直角边的平方分别为25、144,
∴两直角边长分别为$\sqrt{25}=5$,$\sqrt{144}=12$。
由勾股定理得$x=\sqrt{5^{2}+12^{2}}=\sqrt{25 + 144}=\sqrt{169}=13$。
第二个直角三角形:
∵两直角边长均为6,
由勾股定理得$y=\sqrt{6^{2}+6^{2}}=\sqrt{36 + 36}=\sqrt{72}=6\sqrt{2}$。
第三个直角三角形:
∵两直角边长分别为3、4,
由勾股定理得$z=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
答案:$x=13$,$y=6\sqrt{2}$,$z=5$。
第一个直角三角形:
∵两直角边的平方分别为25、144,
∴两直角边长分别为$\sqrt{25}=5$,$\sqrt{144}=12$。
由勾股定理得$x=\sqrt{5^{2}+12^{2}}=\sqrt{25 + 144}=\sqrt{169}=13$。
第二个直角三角形:
∵两直角边长均为6,
由勾股定理得$y=\sqrt{6^{2}+6^{2}}=\sqrt{36 + 36}=\sqrt{72}=6\sqrt{2}$。
第三个直角三角形:
∵两直角边长分别为3、4,
由勾股定理得$z=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
答案:$x=13$,$y=6\sqrt{2}$,$z=5$。
3. 在数轴上画出$\sqrt{10}$对应的点.
答案:解:1. 在数轴上找到原点O,设单位长度为1,取点A表示1。
2. 过点A作数轴的垂线l。
3. 在垂线l上截取AB=3,连接OB。
4. 以点O为圆心,OB长为半径画弧,交数轴正半轴于点C。
点C即为数轴上表示$\sqrt{10}$的点。
2. 过点A作数轴的垂线l。
3. 在垂线l上截取AB=3,连接OB。
4. 以点O为圆心,OB长为半径画弧,交数轴正半轴于点C。
点C即为数轴上表示$\sqrt{10}$的点。
4.(1)如图,一竹竿在离地面6m处折断,竹竿顶部落在离竹竿底部8m处,则竹竿折断前的高度是
(2)如图,一个圆锥的高$AO= 2.4\ cm$,底面半径$OB= 0.7\ cm$,则AB的长是
16
m;(2)如图,一个圆锥的高$AO= 2.4\ cm$,底面半径$OB= 0.7\ cm$,则AB的长是
2.5
cm.答案:4.(1)解:设折断部分长度为$x$m,由勾股定理得$x^{2}=6^{2}+8^{2}$,$x^{2}=36 + 64=100$,$x = 10$(负值舍去),则竹竿折断前高度为$6+10=16$m。16
(2)解:在$Rt\triangle AOB$中,由勾股定理得$AB^{2}=AO^{2}+OB^{2}=2.4^{2}+0.7^{2}=5.76 + 0.49=6.25$,$AB = 2.5$cm。2.5
(2)解:在$Rt\triangle AOB$中,由勾股定理得$AB^{2}=AO^{2}+OB^{2}=2.4^{2}+0.7^{2}=5.76 + 0.49=6.25$,$AB = 2.5$cm。2.5