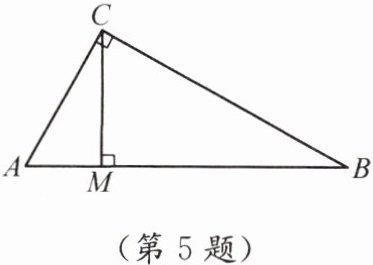
5. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$CM\perp AB$,垂足为M.
(1)若$AC= 6$,$BC= 8$,则CM的长度为多少?
(2)若$AM= 3$,$BM= 12$,则CM的长度为多少?
(1)若$AC= 6$,$BC= 8$,则CM的长度为多少?
(2)若$AM= 3$,$BM= 12$,则CM的长度为多少?

答案:【解析】:
(1) 本题考查勾股定理及面积公式。
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 6$,$BC = 8$。
根据勾股定理$AB^2=AC^2 + BC^2$,可求出斜边$AB$的长度。
再根据三角形面积公式$S=\frac{1}{2}AC× BC=\frac{1}{2}AB× CM$,进而求出$CM$的长度。
(2)本题考查勾股定理的应用。
设$CM = h$,在$Rt\triangle ACM$和$Rt\triangle BCM$中,分别根据勾股定理表示出$AC^2$和$BC^2$。
又因为在$Rt\triangle ABC$中$AC^2+BC^2 = AB^2$,$AB=AM + BM$,从而可以求出$h$的值。
【答案】:
解:(1)
在$Rt\triangle ABC$中,根据勾股定理$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=\sqrt{36 + 64}=\sqrt{100}=10$。
因为$S_{\triangle ABC}=\frac{1}{2}AC× BC=\frac{1}{2}AB× CM$,
即$\frac{1}{2}×6×8=\frac{1}{2}×10× CM$,
$CM=\frac{6×8}{10}=4.8$。
(2)
设$CM = h$。
在$Rt\triangle ACM$中,$AC^{2}=AM^{2}+CM^{2}=3^{2}+h^{2}=9 + h^{2}$。
在$Rt\triangle BCM$中,$BC^{2}=BM^{2}+CM^{2}=12^{2}+h^{2}=144 + h^{2}$。
在$Rt\triangle ABC$中,$AB=AM + BM=3 + 12 = 15$,$AC^{2}+BC^{2}=AB^{2}$,
即$(9 + h^{2})+(144 + h^{2})=15^{2}$,
$2h^{2}+153 = 225$,
$2h^{2}=225 - 153$,
$2h^{2}=72$,
$h^{2}=36$,
解得$h = 6$($h\gt0$),
即$CM = 6$。
综上,答案依次为:(1)$4.8$;(2)$6$。
(1) 本题考查勾股定理及面积公式。
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 6$,$BC = 8$。
根据勾股定理$AB^2=AC^2 + BC^2$,可求出斜边$AB$的长度。
再根据三角形面积公式$S=\frac{1}{2}AC× BC=\frac{1}{2}AB× CM$,进而求出$CM$的长度。
(2)本题考查勾股定理的应用。
设$CM = h$,在$Rt\triangle ACM$和$Rt\triangle BCM$中,分别根据勾股定理表示出$AC^2$和$BC^2$。
又因为在$Rt\triangle ABC$中$AC^2+BC^2 = AB^2$,$AB=AM + BM$,从而可以求出$h$的值。
【答案】:
解:(1)
在$Rt\triangle ABC$中,根据勾股定理$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=\sqrt{36 + 64}=\sqrt{100}=10$。
因为$S_{\triangle ABC}=\frac{1}{2}AC× BC=\frac{1}{2}AB× CM$,
即$\frac{1}{2}×6×8=\frac{1}{2}×10× CM$,
$CM=\frac{6×8}{10}=4.8$。
(2)
设$CM = h$。
在$Rt\triangle ACM$中,$AC^{2}=AM^{2}+CM^{2}=3^{2}+h^{2}=9 + h^{2}$。
在$Rt\triangle BCM$中,$BC^{2}=BM^{2}+CM^{2}=12^{2}+h^{2}=144 + h^{2}$。
在$Rt\triangle ABC$中,$AB=AM + BM=3 + 12 = 15$,$AC^{2}+BC^{2}=AB^{2}$,
即$(9 + h^{2})+(144 + h^{2})=15^{2}$,
$2h^{2}+153 = 225$,
$2h^{2}=225 - 153$,
$2h^{2}=72$,
$h^{2}=36$,
解得$h = 6$($h\gt0$),
即$CM = 6$。
综上,答案依次为:(1)$4.8$;(2)$6$。
6. 如图,$\triangle ABC和\triangle DEF$都不是直角三角形,分别以$\triangle ABC和\triangle DEF$的各边为一边向三角形外部作正方形,其中两个小正方形面积的和等于大正方形的面积吗?说明理由.


答案:解:对于△ABC:
设每个小方格边长为1,
以AB为边的正方形面积:3×3=9,
以BC为边的正方形面积:2×2 + 2×2=8(通过数格子或割补法),
以AC为边的正方形面积:1×1 + 2×2=5,
9+5=14≠8,9+8=17≠5,5+8=13≠9,故两个小正方形面积和不等于大正方形面积。
对于△DEF:
以DE为边的正方形面积:4×4=16,
以EF为边的正方形面积:2×2=4,
以DF为边的正方形面积:4×4 + 2×2=20(通过数格子或割补法),
16+4=20,故两个小正方形面积和等于大正方形面积。
结论:△ABC的两个小正方形面积的和不等于大正方形的面积;△DEF的两个小正方形面积的和等于大正方形的面积。
设每个小方格边长为1,
以AB为边的正方形面积:3×3=9,
以BC为边的正方形面积:2×2 + 2×2=8(通过数格子或割补法),
以AC为边的正方形面积:1×1 + 2×2=5,
9+5=14≠8,9+8=17≠5,5+8=13≠9,故两个小正方形面积和不等于大正方形面积。
对于△DEF:
以DE为边的正方形面积:4×4=16,
以EF为边的正方形面积:2×2=4,
以DF为边的正方形面积:4×4 + 2×2=20(通过数格子或割补法),
16+4=20,故两个小正方形面积和等于大正方形面积。
结论:△ABC的两个小正方形面积的和不等于大正方形的面积;△DEF的两个小正方形面积的和等于大正方形的面积。
7. 如图,正方形M经过2次“生长”形成“勾股树”,其中所有的四边形都是正方形,面积分别记作$S_{M},S_{A},S_{B},S_{C},S_{D},S_{E},S_{F}$,所有的三角形都是直角三角形.
(1)正方形M,E,F的面积$S_{M},S_{E},S_{F}$之间有什么关系?
(2)第2次“生长”出来的4个正方形A,B,C,D的面积与正方形M的面积有什么关系?
(3)随着这棵勾股树的不断“生长”,请你提出一个问题,并给出答案.

(1)正方形M,E,F的面积$S_{M},S_{E},S_{F}$之间有什么关系?
(2)第2次“生长”出来的4个正方形A,B,C,D的面积与正方形M的面积有什么关系?
(3)随着这棵勾股树的不断“生长”,请你提出一个问题,并给出答案.

答案:(1)解:设与正方形E、F相邻的直角三角形的两条直角边分别为a、b,斜边为c。
由勾股定理得:$a^2 + b^2 = c^2$。
因为$S_E = a^2$,$S_F = b^2$,$S_M = c^2$,
所以$S_M = S_E + S_F$。
(2)解:同理,设与正方形A、B相邻的直角三角形直角边为$a_1$、$b_1$,斜边为$c_1$(即正方形E的边长),则$S_A + S_B = S_E$;
设与正方形C、D相邻的直角三角形直角边为$a_2$、$b_2$,斜边为$c_2$(即正方形F的边长),则$S_C + S_D = S_F$。
由(1)知$S_M = S_E + S_F$,
所以$S_A + S_B + S_C + S_D = S_E + S_F = S_M$。
(3)解:问题:第1次“生长”出来的2个正方形E、F的面积之和与正方形M的面积有什么关系?
答案:$S_E + S_F = S_M$。
由勾股定理得:$a^2 + b^2 = c^2$。
因为$S_E = a^2$,$S_F = b^2$,$S_M = c^2$,
所以$S_M = S_E + S_F$。
(2)解:同理,设与正方形A、B相邻的直角三角形直角边为$a_1$、$b_1$,斜边为$c_1$(即正方形E的边长),则$S_A + S_B = S_E$;
设与正方形C、D相邻的直角三角形直角边为$a_2$、$b_2$,斜边为$c_2$(即正方形F的边长),则$S_C + S_D = S_F$。
由(1)知$S_M = S_E + S_F$,
所以$S_A + S_B + S_C + S_D = S_E + S_F = S_M$。
(3)解:问题:第1次“生长”出来的2个正方形E、F的面积之和与正方形M的面积有什么关系?
答案:$S_E + S_F = S_M$。