1. 在△ABC中,∠C=90°,两条直角边分别为a,b,斜边为c.
(1) 已知a=3,b=4,则c=
(2) 已知c=13,b=5,则a=
(3) 已知c=17,a=15,则b=
(4) 已知a+b=14,ab=48,则c=
(1) 已知a=3,b=4,则c=
5
;(2) 已知c=13,b=5,则a=
12
;(3) 已知c=17,a=15,则b=
8
;(4) 已知a+b=14,ab=48,则c=
10
.答案:【解析】:
1.本题主要考查勾股定理的应用。在直角三角形中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a$、$b$为直角边,$c$为斜边)来分别计算各小题。
(1)已知$a = 3$,$b = 4$,将其代入勾股定理$c=\sqrt{a^{2}+b^{2}}=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
(2)已知$c = 13$,$b = 5$,由勾股定理$a=\sqrt{c^{2}-b^{2}}=\sqrt{13^{2}-5^{2}}=\sqrt{169 - 25}=\sqrt{144}=12$。
(3)已知$c = 17$,$a = 15$,同理$b=\sqrt{c^{2}-a^{2}}=\sqrt{17^{2}-15^{2}}=\sqrt{289 - 225}=\sqrt{64}=8$。
(4)已知$a + b = 14$,$ab = 48$,先求$a^{2}+b^{2}$,根据完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$,则$a^{2}+b^{2}=(a + b)^{2}-2ab$,把$a + b = 14$,$ab = 48$代入可得$a^{2}+b^{2}=14^{2}-2×48=196 - 96 = 100$,所以$c=\sqrt{a^{2}+b^{2}}=\sqrt{100}=10$。
1.本题主要考查勾股定理的应用。在直角三角形中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a$、$b$为直角边,$c$为斜边)来分别计算各小题。
(1)已知$a = 3$,$b = 4$,将其代入勾股定理$c=\sqrt{a^{2}+b^{2}}=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
(2)已知$c = 13$,$b = 5$,由勾股定理$a=\sqrt{c^{2}-b^{2}}=\sqrt{13^{2}-5^{2}}=\sqrt{169 - 25}=\sqrt{144}=12$。
(3)已知$c = 17$,$a = 15$,同理$b=\sqrt{c^{2}-a^{2}}=\sqrt{17^{2}-15^{2}}=\sqrt{289 - 225}=\sqrt{64}=8$。
(4)已知$a + b = 14$,$ab = 48$,先求$a^{2}+b^{2}$,根据完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$,则$a^{2}+b^{2}=(a + b)^{2}-2ab$,把$a + b = 14$,$ab = 48$代入可得$a^{2}+b^{2}=14^{2}-2×48=196 - 96 = 100$,所以$c=\sqrt{a^{2}+b^{2}}=\sqrt{100}=10$。
【答案】:
1.(1)$5$;(2)$12$;(3)$8$;(4)$10$。
2. 在Rt△ABC中,∠C=90°,AB=25,AC=7,则△ABC的面积为_________.
答案:
@@2.本题可先根据勾股定理求出$BC$边上的高$AD$对应的另一条直角边$BC$的长度,再根据三角形面积公式求解。
已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 25$,$AC = 7$,由勾股定理$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{25^{2}-7^{2}}=\sqrt{625 - 49}=\sqrt{576}=24$。
根据三角形面积公式$S=\frac{1}{2}×底×高$,这里以$AC$为高,$BC$为底,则$S_{\triangle ABC}=\frac{1}{2}× AC× BC=\frac{1}{2}×7×24 = 84$。
【答案】:2.$84$。
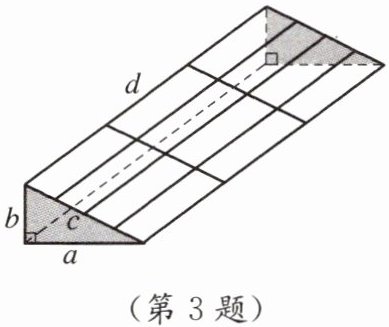
3. 如图,要修建一个育苗棚,棚宽a为2 m,高b为1.5 m,长d为10 m.覆盖在棚顶的塑料薄膜的面积是_________m².

答案:
@@3.本题可先根据勾股定理求出棚顶斜边的长度,再根据矩形面积公式求出塑料薄膜的面积。
棚顶是一个长方形,宽$a = 2m$,高$b =@@1.5m$,根据勾股定理,棚顶斜边长度$l=\sqrt{a^{2}+b^{2}}=\sqrt{2^{2}+1.5^{2}}=\sqrt{4 +@@2.25}=\sqrt{6.25}=2.5m$。
棚长$d = 10m$,覆盖在棚顶的塑料薄膜的面积为斜边长度乘以棚长,即$S =@@2.5×10 = 25m^{2}$。
【答案】:3.$25$。
4. 如图,在△ABC中,AD⊥BC,垂足为D,AB=AC=5,BC=6.AD=_________,△ABC的面积为_________.


答案:
@@4.本题可先根据等腰三角形三线合一的性质求出$BD$的长度,再利用勾股定理求出$AD$的长度,最后根据三角形面积公式求出$\triangle ABC$的面积。
因为$AB = AC = 5$,$AD\perp BC$,根据等腰三角形三线合一,$D$为$BC$中点,所以$BD=\frac{1}{2}BC=\frac{1}{2}×6 = 3m$。
在$Rt\triangle ABD$中,由勾股定理$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4m$。
根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}× BC× AD=\frac{1}{2}×6×4 = 12$。
【答案】:4.$4$;$12$。
5. 已知一个直角三角形的两边长分别为3和4,则第三边的长为_________.
答案:
@@5.本题需要分情况讨论,因为不确定$3$和$4$是直角边还是一条直角边一条斜边。
当$3$和$4$为直角边时,根据勾股定理,第三边(斜边)长度为$\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
当$4$为斜边,$3$为直角边时,第三边(另一条直角边)长度为$\sqrt{4^{2}-3^{2}}=\sqrt{16 - 9}=\sqrt{7}$。
【答案】:5.$5$或$\sqrt{7}$。
6. 我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式,这种方法称为“无字证明”,它比严谨的数学证明更为优雅和有条理.下面是用三块全等的直角三角形移、拼、补所形成的“无字证明”图形.
(1) 图①可以用来证明你学过的什么定理?请写出定理的内容.
(2) 已知直角三角形的直角边长分别为a,b,斜边长为c,图①、图②的面积相等,请你根据图形证明(1)中的定理.

(1) 图①可以用来证明你学过的什么定理?请写出定理的内容.
(2) 已知直角三角形的直角边长分别为a,b,斜边长为c,图①、图②的面积相等,请你根据图形证明(1)中的定理.

答案:
@@6.本题主要考查勾股定理的证明。
(1)图①可以用来证明勾股定理,内容为:在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方,即如果直角三角形的两条直角边长度分别是$a$和$b$,斜边长度是$c$,那么$a^{2}+b^{2}=c^{2}$。
(2)图①中,大正方形的边长为$c$,根据正方形面积公式,其面积$S = c^{2}$。同时,大正方形面积又等于四个直角三角形的面积与中间小正方形面积之和。四个直角三角形面积之和为$4×\frac{1}{2}ab = 2ab$,小正方形边长为$(a - b)$,其面积为$(a - b)^{2}$,所以大正方形面积$S = 2ab+(a - b)^{2}$,展开$(a - b)^{2}=a^{2}-2ab + b^{2}$,则$S = 2ab+a^{2}-2ab + b^{2}=a^{2}+b^{2}$。因为大正方形面积有两种表示方法,所以$a^{2}+b^{2}=c^{2}$。
【答案】:
6.(1)勾股定理,在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方。(2)证明过程如上述解析。