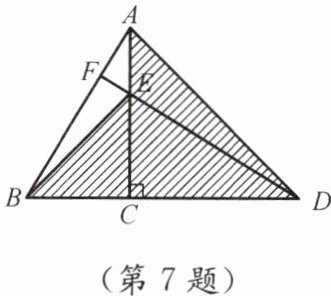
7. 如图,在△ABD中,AC⊥BD,垂足为C,点E在AC上,连接BE,DE,DE的延长线交AB于点F,DE=AB,∠CAD=45°.
(1) 求证:DF⊥AB.
(2) 利用图中阴影部分面积完成勾股定理的证明.
已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.
求证:a²+b²=c².
(1) 求证:DF⊥AB.
(2) 利用图中阴影部分面积完成勾股定理的证明.
已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.
求证:a²+b²=c².

答案:1. (1)证明:
因为$AC\perp BD$,$\angle CAD = 45^{\circ}$,所以$\angle ACD=\angle ACB = 90^{\circ}$,$\triangle ACD$是等腰直角三角形,即$AC = CD$。
在$Rt\triangle ABC$和$Rt\triangle DEC$中,$\left\{\begin{array}{l}AB = DE\\AC = CD\end{array}\right.$。
根据$HL$(斜边 - 直角边)定理,$Rt\triangle ABC\cong Rt\triangle DEC$。
所以$\angle BAC=\angle EDC$。
因为$\angle EDC+\angle DEC = 90^{\circ}$,$\angle DEC=\angle AEF$(对顶角相等)。
所以$\angle BAC+\angle AEF = 90^{\circ}$。
在$\triangle AEF$中,$\angle AFE=180^{\circ}-(\angle BAC + \angle AEF)=90^{\circ}$,即$DF\perp AB$。
2. (2)证明:
因为$S_{\triangle BCE}+S_{\triangle ACD}=S_{\triangle ABD}-S_{\triangle ABE}$。
由(1)知$Rt\triangle ABC\cong Rt\triangle DEC$,$S_{\triangle ABC}=S_{\triangle DEC}$,$AC = CD=b$,$BC = CE=a$,$AB = DE = c$。
$S_{\triangle BCE}=\frac{1}{2}a^{2}$,$S_{\triangle ACD}=\frac{1}{2}b^{2}$,$S_{\triangle ABD}=\frac{1}{2}c\cdot DF$,$S_{\triangle ABE}=\frac{1}{2}c\cdot EF$,且$DF = DE + EF=c + EF$。
又$S_{\triangle BCE}+S_{\triangle ACD}=\frac{1}{2}a^{2}+\frac{1}{2}b^{2}$,$S_{\triangle ABD}-S_{\triangle ABE}=\frac{1}{2}c(DF - EF)=\frac{1}{2}c^{2}$。
所以$a^{2}+b^{2}=c^{2}$。
综上,(1)得证$DF\perp AB$;(2)得证$a^{2}+b^{2}=c^{2}$。
因为$AC\perp BD$,$\angle CAD = 45^{\circ}$,所以$\angle ACD=\angle ACB = 90^{\circ}$,$\triangle ACD$是等腰直角三角形,即$AC = CD$。
在$Rt\triangle ABC$和$Rt\triangle DEC$中,$\left\{\begin{array}{l}AB = DE\\AC = CD\end{array}\right.$。
根据$HL$(斜边 - 直角边)定理,$Rt\triangle ABC\cong Rt\triangle DEC$。
所以$\angle BAC=\angle EDC$。
因为$\angle EDC+\angle DEC = 90^{\circ}$,$\angle DEC=\angle AEF$(对顶角相等)。
所以$\angle BAC+\angle AEF = 90^{\circ}$。
在$\triangle AEF$中,$\angle AFE=180^{\circ}-(\angle BAC + \angle AEF)=90^{\circ}$,即$DF\perp AB$。
2. (2)证明:
因为$S_{\triangle BCE}+S_{\triangle ACD}=S_{\triangle ABD}-S_{\triangle ABE}$。
由(1)知$Rt\triangle ABC\cong Rt\triangle DEC$,$S_{\triangle ABC}=S_{\triangle DEC}$,$AC = CD=b$,$BC = CE=a$,$AB = DE = c$。
$S_{\triangle BCE}=\frac{1}{2}a^{2}$,$S_{\triangle ACD}=\frac{1}{2}b^{2}$,$S_{\triangle ABD}=\frac{1}{2}c\cdot DF$,$S_{\triangle ABE}=\frac{1}{2}c\cdot EF$,且$DF = DE + EF=c + EF$。
又$S_{\triangle BCE}+S_{\triangle ACD}=\frac{1}{2}a^{2}+\frac{1}{2}b^{2}$,$S_{\triangle ABD}-S_{\triangle ABE}=\frac{1}{2}c(DF - EF)=\frac{1}{2}c^{2}$。
所以$a^{2}+b^{2}=c^{2}$。
综上,(1)得证$DF\perp AB$;(2)得证$a^{2}+b^{2}=c^{2}$。