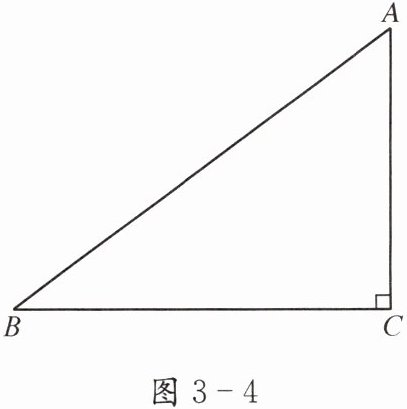
如图 3-4,在 Rt△ABC 中,∠C= 90°,AC= 3 cm,BC= 4 cm. 画一个△DEF,使 DF= 3 cm,EF= 4 cm,DE= 5 cm. △ABC 与△DEF 全等吗? △DEF 是直角三角形吗? 请说明理由.

答案:解:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
由勾股定理得AB²=AC²+BC²=3²+4²=25,
∴AB=5cm。
△ABC与△DEF不全等。
理由:△ABC中AC=3cm,BC=4cm,AB=5cm;△DEF中DF=3cm,EF=4cm,DE=5cm。两三角形对应边不一定相等,故不全等。
△DEF是直角三角形。
理由:在△DEF中,DF=3cm,EF=4cm,DE=5cm,
∵DF²+EF²=3²+4²=25,DE²=5²=25,
∴DF²+EF²=DE²,
由勾股定理的逆定理得△DEF是直角三角形,且∠F=90°。
由勾股定理得AB²=AC²+BC²=3²+4²=25,
∴AB=5cm。
△ABC与△DEF不全等。
理由:△ABC中AC=3cm,BC=4cm,AB=5cm;△DEF中DF=3cm,EF=4cm,DE=5cm。两三角形对应边不一定相等,故不全等。
△DEF是直角三角形。
理由:在△DEF中,DF=3cm,EF=4cm,DE=5cm,
∵DF²+EF²=3²+4²=25,DE²=5²=25,
∴DF²+EF²=DE²,
由勾股定理的逆定理得△DEF是直角三角形,且∠F=90°。
例1 如图3-5,在四边形ABCD中,AB= 20,AD= 15,CD= 7,BC= 24,∠A= 90°.求证:∠C= 90°.


答案:【解析】:
本题主要考查勾股定理的逆定理,即如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形。我们可以先通过已知条件求出$BD$的长度,再分别在$\triangle ABD$和$\triangle BCD$中运用勾股定理及其逆定理来证明$\angle C = 90^{\circ}$。
1. 在$Rt\triangle ABD$中,已知$\angle A = 90^{\circ}$,$AB = 20$,$AD = 15$,根据勾股定理$BD^{2}=AB^{2}+AD^{2}$,可求出$BD$的长度。
2. 计算出$BD$的长度后,再在$\triangle BCD$中,计算$CD^{2}+BC^{2}$和$BD^{2}$的值,比较它们是否相等,若相等,则根据勾股定理的逆定理可证明$\angle C = 90^{\circ}$。
【答案】:
证明:
连接$BD$。
在$Rt\triangle ABD$中,因为$\angle A = 90^{\circ}$,$AB = 20$,$AD = 15$,根据勾股定理可得:
$BD^{2}=AB^{2}+AD^{2}=20^{2}+15^{2}=400 + 225 = 625$,
所以$BD=\sqrt{625}=25$。
在$\triangle BCD$中,已知$CD = 7$,$BC = 24$,则$CD^{2}+BC^{2}=7^{2}+24^{2}=49 + 576 = 625$,
而$BD^{2}=625$,所以$CD^{2}+BC^{2}=BD^{2}$。
根据勾股定理的逆定理,可知$\triangle BCD$是直角三角形,且$\angle C = 90^{\circ}$。
综上,$\angle C = 90^{\circ}$得证。
本题主要考查勾股定理的逆定理,即如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形。我们可以先通过已知条件求出$BD$的长度,再分别在$\triangle ABD$和$\triangle BCD$中运用勾股定理及其逆定理来证明$\angle C = 90^{\circ}$。
1. 在$Rt\triangle ABD$中,已知$\angle A = 90^{\circ}$,$AB = 20$,$AD = 15$,根据勾股定理$BD^{2}=AB^{2}+AD^{2}$,可求出$BD$的长度。
2. 计算出$BD$的长度后,再在$\triangle BCD$中,计算$CD^{2}+BC^{2}$和$BD^{2}$的值,比较它们是否相等,若相等,则根据勾股定理的逆定理可证明$\angle C = 90^{\circ}$。
【答案】:
证明:
连接$BD$。
在$Rt\triangle ABD$中,因为$\angle A = 90^{\circ}$,$AB = 20$,$AD = 15$,根据勾股定理可得:
$BD^{2}=AB^{2}+AD^{2}=20^{2}+15^{2}=400 + 225 = 625$,
所以$BD=\sqrt{625}=25$。
在$\triangle BCD$中,已知$CD = 7$,$BC = 24$,则$CD^{2}+BC^{2}=7^{2}+24^{2}=49 + 576 = 625$,
而$BD^{2}=625$,所以$CD^{2}+BC^{2}=BD^{2}$。
根据勾股定理的逆定理,可知$\triangle BCD$是直角三角形,且$\angle C = 90^{\circ}$。
综上,$\angle C = 90^{\circ}$得证。
例2 一个三角形的三边比为1:√3:2,这个三角形是直角三角形吗? 请证明你的结论.
答案:【解析】:
本题主要考察勾股定理的逆定理,即如果三角形三边满足勾股定理,那么三角形是直角三角形。
首先,我们设三角形的三边分别为$a$,$\sqrt{3}a$,$2a$,其中$a > 0$。
根据勾股定理的逆定理,如果$a^{2} + {(\sqrt{3}a)}^{2} = {(2a)}^{2}$,那么这个三角形就是直角三角形。
接下来,我们将进行具体的计算来验证这个等式是否成立。
【答案】:
证明:
设三角形的三边分别为$a$,$\sqrt{3}a$,$2a$,其中$a > 0$,
我们有:
$a^{2} + {(\sqrt{3}a)}^{2}$
$= a^{2} + 3a^{2}$
$= 4a^{2}$
又因为${(2a)}^{2} = 4a^{2}$,
所以$a^{2} + {(\sqrt{3}a)}^{2} = {(2a)}^{2}$,
因此,这个三角形是直角三角形。
本题主要考察勾股定理的逆定理,即如果三角形三边满足勾股定理,那么三角形是直角三角形。
首先,我们设三角形的三边分别为$a$,$\sqrt{3}a$,$2a$,其中$a > 0$。
根据勾股定理的逆定理,如果$a^{2} + {(\sqrt{3}a)}^{2} = {(2a)}^{2}$,那么这个三角形就是直角三角形。
接下来,我们将进行具体的计算来验证这个等式是否成立。
【答案】:
证明:
设三角形的三边分别为$a$,$\sqrt{3}a$,$2a$,其中$a > 0$,
我们有:
$a^{2} + {(\sqrt{3}a)}^{2}$
$= a^{2} + 3a^{2}$
$= 4a^{2}$
又因为${(2a)}^{2} = 4a^{2}$,
所以$a^{2} + {(\sqrt{3}a)}^{2} = {(2a)}^{2}$,
因此,这个三角形是直角三角形。
1. 如果三角形的三边长a,b,c(a≤b≤c)满足
$a^{2} + b^{2} = c^{2}$
,那么这个三角形是直角三角形.答案:【解析】:
本题考查的是勾股定理的逆定理。勾股定理的逆定理表明,如果一个三角形的三边长$a, b, c$(其中$a \leq b \leq c$)满足$a^{2} + b^{2} = c^{2}$,那么这个三角形一定是直角三角形。
【答案】:
$a^{2} + b^{2} = c^{2}$
本题考查的是勾股定理的逆定理。勾股定理的逆定理表明,如果一个三角形的三边长$a, b, c$(其中$a \leq b \leq c$)满足$a^{2} + b^{2} = c^{2}$,那么这个三角形一定是直角三角形。
【答案】:
$a^{2} + b^{2} = c^{2}$