2. 将下列长度的3根木棒首尾依次连接,能组成直角三角形的是(
A.1,2,3
B.1/3,1/4,1/5
C.√3,√4,√5
D.6,8,10
D
).A.1,2,3
B.1/3,1/4,1/5
C.√3,√4,√5
D.6,8,10
答案:【解析】:
本题考察的是勾股定理的逆定理,即如果三角形三边满足勾股定理,即最长边的平方等于其他两边的平方和,那么这个三角形就是直角三角形。
我们需要将每个选项中的三边长度代入勾股定理进行验证。
A选项:$1^2 + 2^2 = 1 + 4 = 5$,而$3^2 = 9$,因为5不等于9,所以A选项不能构成直角三角形。
B选项:$\left(\frac{1}{3}\right)^2 + \left(\frac{1}{4}\right)^2 = \frac{1}{9} + \frac{1}{16} = \frac{25}{144}$,而$\left(\frac{1}{5}\right)^2 = \frac{1}{25}$,因为$\frac{25}{144}$不等于$\frac{1}{25}$,所以B选项不能构成直角三角形。
C选项:$(\sqrt{3})^2 + (\sqrt{4})^2 = 3 + 4 = 7$,而$(\sqrt{5})^2 = 5$,因为7不等于5,所以C选项不能构成直角三角形。
D选项:$6^2 + 8^2 = 36 + 64 = 100$,而$10^2 = 100$,因为两边平方和等于最长边的平方,所以D选项能构成直角三角形。
【答案】:
D
本题考察的是勾股定理的逆定理,即如果三角形三边满足勾股定理,即最长边的平方等于其他两边的平方和,那么这个三角形就是直角三角形。
我们需要将每个选项中的三边长度代入勾股定理进行验证。
A选项:$1^2 + 2^2 = 1 + 4 = 5$,而$3^2 = 9$,因为5不等于9,所以A选项不能构成直角三角形。
B选项:$\left(\frac{1}{3}\right)^2 + \left(\frac{1}{4}\right)^2 = \frac{1}{9} + \frac{1}{16} = \frac{25}{144}$,而$\left(\frac{1}{5}\right)^2 = \frac{1}{25}$,因为$\frac{25}{144}$不等于$\frac{1}{25}$,所以B选项不能构成直角三角形。
C选项:$(\sqrt{3})^2 + (\sqrt{4})^2 = 3 + 4 = 7$,而$(\sqrt{5})^2 = 5$,因为7不等于5,所以C选项不能构成直角三角形。
D选项:$6^2 + 8^2 = 36 + 64 = 100$,而$10^2 = 100$,因为两边平方和等于最长边的平方,所以D选项能构成直角三角形。
【答案】:
D
3. 以下列各组数为三边边长的三角形是否为直角三角形? 为什么?
(1)5,12,13;
(2)2/3,2/3,1;
(3)4/3,5/3,1;
(4)6.5,6,2.5.
(1)5,12,13;
(2)2/3,2/3,1;
(3)4/3,5/3,1;
(4)6.5,6,2.5.
答案:(1)解:是直角三角形。
因为$5^{2}+12^{2}=25 + 144=169$,$13^{2}=169$,
所以$5^{2}+12^{2}=13^{2}$,
根据勾股定理的逆定理,该三角形是直角三角形。
(2)解:不是直角三角形。
因为$(\frac{2}{3})^{2}+(\frac{2}{3})^{2}=\frac{4}{9}+\frac{4}{9}=\frac{8}{9}$,$1^{2}=1=\frac{9}{9}$,
$\frac{8}{9}\neq\frac{9}{9}$,即$(\frac{2}{3})^{2}+(\frac{2}{3})^{2}\neq1^{2}$,
所以该三角形不是直角三角形。
(3)解:是直角三角形。
因为$1^{2}+(\frac{4}{3})^{2}=1+\frac{16}{9}=\frac{25}{9}$,$(\frac{5}{3})^{2}=\frac{25}{9}$,
所以$1^{2}+(\frac{4}{3})^{2}=(\frac{5}{3})^{2}$,
根据勾股定理的逆定理,该三角形是直角三角形。
(4)解:是直角三角形。
因为$2.5^{2}+6^{2}=6.25 + 36=42.25$,$6.5^{2}=42.25$,
所以$2.5^{2}+6^{2}=6.5^{2}$,
根据勾股定理的逆定理,该三角形是直角三角形。
因为$5^{2}+12^{2}=25 + 144=169$,$13^{2}=169$,
所以$5^{2}+12^{2}=13^{2}$,
根据勾股定理的逆定理,该三角形是直角三角形。
(2)解:不是直角三角形。
因为$(\frac{2}{3})^{2}+(\frac{2}{3})^{2}=\frac{4}{9}+\frac{4}{9}=\frac{8}{9}$,$1^{2}=1=\frac{9}{9}$,
$\frac{8}{9}\neq\frac{9}{9}$,即$(\frac{2}{3})^{2}+(\frac{2}{3})^{2}\neq1^{2}$,
所以该三角形不是直角三角形。
(3)解:是直角三角形。
因为$1^{2}+(\frac{4}{3})^{2}=1+\frac{16}{9}=\frac{25}{9}$,$(\frac{5}{3})^{2}=\frac{25}{9}$,
所以$1^{2}+(\frac{4}{3})^{2}=(\frac{5}{3})^{2}$,
根据勾股定理的逆定理,该三角形是直角三角形。
(4)解:是直角三角形。
因为$2.5^{2}+6^{2}=6.25 + 36=42.25$,$6.5^{2}=42.25$,
所以$2.5^{2}+6^{2}=6.5^{2}$,
根据勾股定理的逆定理,该三角形是直角三角形。
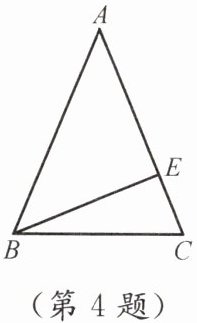
4. 如图,在△ABC中,AB= AC,点E在边AC上,CE= 5,BC= 13,BE= 12.
(1)判断△ABE的形状,并说明理由;
(2)求边AB的长.
(1)判断△ABE的形状,并说明理由;
(2)求边AB的长.

答案:(1)△ABE是直角三角形,理由如下:
在△BEC中,CE=5,BE=12,BC=13
∵5²+12²=25+144=169=13²
∴CE²+BE²=BC²
∴△BEC是直角三角形,∠BEC=90°
∵∠AEB+∠BEC=180°
∴∠AEB=180°-∠BEC=90°
∴△ABE是直角三角形
(2)设AB=AC=x
∵CE=5
∴AE=AC-CE=x-5
由(1)知△ABE是直角三角形,∠AEB=90°
∴根据勾股定理,得AE²+BE²=AB²
即(x-5)²+12²=x²
展开得x²-10x+25+144=x²
移项合并得-10x+169=0
解得10x=169
x=16.9
即AB的长为16.9
在△BEC中,CE=5,BE=12,BC=13
∵5²+12²=25+144=169=13²
∴CE²+BE²=BC²
∴△BEC是直角三角形,∠BEC=90°
∵∠AEB+∠BEC=180°
∴∠AEB=180°-∠BEC=90°
∴△ABE是直角三角形
(2)设AB=AC=x
∵CE=5
∴AE=AC-CE=x-5
由(1)知△ABE是直角三角形,∠AEB=90°
∴根据勾股定理,得AE²+BE²=AB²
即(x-5)²+12²=x²
展开得x²-10x+25+144=x²
移项合并得-10x+169=0
解得10x=169
x=16.9
即AB的长为16.9
5. 如图,每个小正方形的边长都为1,A,B,C,D均在网格格点上.
(1)求四边形ABCD的面积.
(2)∠C是直角吗? 为什么?

(1)求四边形ABCD的面积.
(2)∠C是直角吗? 为什么?

答案:(1)解:四边形ABCD的面积=大矩形面积-四个直角三角形面积
大矩形长为5,宽为4,面积=5×4=20
S△ABF=$\frac{1}{2}$×1×4=2,S△BCG=$\frac{1}{2}$×2×3=3,S△CDH=$\frac{1}{2}$×2×2=2,S△ADE=$\frac{1}{2}$×3×3=4.5
四边形ABCD面积=20-2-3-2-4.5=8.5
(2)解:不是直角。
BC2=22+32=13,CD2=22+22=8,BD2=12+42=17
∵13+8=21≠17,∴BC2+CD2≠BD2,故∠C不是直角。
大矩形长为5,宽为4,面积=5×4=20
S△ABF=$\frac{1}{2}$×1×4=2,S△BCG=$\frac{1}{2}$×2×3=3,S△CDH=$\frac{1}{2}$×2×2=2,S△ADE=$\frac{1}{2}$×3×3=4.5
四边形ABCD面积=20-2-3-2-4.5=8.5
(2)解:不是直角。
BC2=22+32=13,CD2=22+22=8,BD2=12+42=17
∵13+8=21≠17,∴BC2+CD2≠BD2,故∠C不是直角。