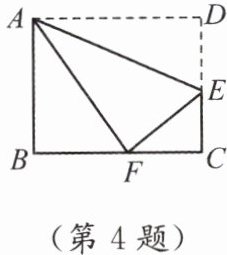
4. 如图,一张矩形纸片ABCD的宽AB为8 cm,长BC为10 cm.折叠这张矩形纸片,使顶点D落在边BC上的点F处(折痕为AE).此时CE有多长?

答案:解:∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,∠B=∠C=90°。
由折叠性质得:AF=AD=10cm,EF=DE。
设CE=x cm,则DE=CD-CE=(8-x)cm,EF=(8-x)cm。
在Rt△ABF中,AB=8cm,AF=10cm,
根据勾股定理得:BF²=AF²-AB²=10²-8²=36,
∴BF=6cm。
∵BC=10cm,
∴CF=BC-BF=10-6=4cm。
在Rt△EFC中,CF=4cm,CE=x cm,EF=(8-x)cm,
根据勾股定理得:CE²+CF²=EF²,
即x²+4²=(8-x)²,
解得x=3。
答:CE的长为3cm。
∴AD=BC=10cm,CD=AB=8cm,∠B=∠C=90°。
由折叠性质得:AF=AD=10cm,EF=DE。
设CE=x cm,则DE=CD-CE=(8-x)cm,EF=(8-x)cm。
在Rt△ABF中,AB=8cm,AF=10cm,
根据勾股定理得:BF²=AF²-AB²=10²-8²=36,
∴BF=6cm。
∵BC=10cm,
∴CF=BC-BF=10-6=4cm。
在Rt△EFC中,CF=4cm,CE=x cm,EF=(8-x)cm,
根据勾股定理得:CE²+CF²=EF²,
即x²+4²=(8-x)²,
解得x=3。
答:CE的长为3cm。
5. 如图,一个长方体木块的长是15 cm,宽是10 cm,高是20 cm,点B到点C的距离是5 cm.如果一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路程是多少?


答案:解:将长方体表面展开,分三种情况讨论:
情况1:展开前面和上面
此时,水平方向长度为15 cm,竖直方向长度为20 + 5 = 25 cm
路程$d_1 = \sqrt{15^2 + 25^2} = \sqrt{225 + 625} = \sqrt{850} \approx 29.15$ cm
情况2:展开前面和右面
此时,水平方向长度为15 + 5 = 20 cm,竖直方向长度为20 cm
路程$d_2 = \sqrt{20^2 + 20^2} = \sqrt{400 + 400} = \sqrt{800} = 20\sqrt{2} \approx 28.28$ cm
情况3:展开左面和上面
此时,水平方向长度为10 + 15 = 25 cm,竖直方向长度为20 - 5 = 15 cm(与情况1相同,路程$d_3 = d_1$)
比较$d_1$、$d_2$,最短路程为$20\sqrt{2}$ cm,即约28.28 cm,精确值为$20\sqrt{2}$ cm。
答:最短路程是$20\sqrt{2}$ cm。
情况1:展开前面和上面
此时,水平方向长度为15 cm,竖直方向长度为20 + 5 = 25 cm
路程$d_1 = \sqrt{15^2 + 25^2} = \sqrt{225 + 625} = \sqrt{850} \approx 29.15$ cm
情况2:展开前面和右面
此时,水平方向长度为15 + 5 = 20 cm,竖直方向长度为20 cm
路程$d_2 = \sqrt{20^2 + 20^2} = \sqrt{400 + 400} = \sqrt{800} = 20\sqrt{2} \approx 28.28$ cm
情况3:展开左面和上面
此时,水平方向长度为10 + 15 = 25 cm,竖直方向长度为20 - 5 = 15 cm(与情况1相同,路程$d_3 = d_1$)
比较$d_1$、$d_2$,最短路程为$20\sqrt{2}$ cm,即约28.28 cm,精确值为$20\sqrt{2}$ cm。
答:最短路程是$20\sqrt{2}$ cm。
6. 在勾股定理的学习中,我们认识到以Rt△ABC的三边为边长的3个正方形的面积之间的关系(图①).在课本习题3.3第4题的探索中,我们得到以Rt△ABC的三边为直径的3个半圆的面积之间的关系(图②).
(1)分别写出图①中3个正方形、图②中3个半圆的面积关系.
(2)通过这两个图形的探索,你有什么发现?设计一个类似的问题,并给出解答.

(1)分别写出图①中3个正方形、图②中3个半圆的面积关系.
(2)通过这两个图形的探索,你有什么发现?设计一个类似的问题,并给出解答.

答案:(1)设Rt△ABC的两条直角边为a、b,斜边为c。
图①中3个正方形的面积关系:以a为边长的正方形面积+以b为边长的正方形面积=以c为边长的正方形面积,即$a^2 + b^2 = c^2$。
图②中3个半圆的面积关系:以a为直径的半圆面积+以b为直径的半圆面积=以c为直径的半圆面积,即$\frac{1}{2}\pi(\frac{a}{2})^2 + \frac{1}{2}\pi(\frac{b}{2})^2 = \frac{1}{2}\pi(\frac{c}{2})^2$。
(2)发现:以直角三角形三边为对应边的图形(如正方形、半圆),若这些图形的面积与对应边长的平方成正比,则两直角边上图形面积之和等于斜边上图形的面积。
设计问题:以Rt△ABC的三边为边长的3个等边三角形的面积之间有什么关系?
解答:设Rt△ABC的两条直角边为a、b,斜边为c,等边三角形面积公式为$\frac{\sqrt{3}}{4}×边长^2$。则以a、b为边长的等边三角形面积之和为$\frac{\sqrt{3}}{4}a^2 + \frac{\sqrt{3}}{4}b^2 = \frac{\sqrt{3}}{4}(a^2 + b^2)$,因为$a^2 + b^2 = c^2$,所以两直角边上等边三角形面积之和等于斜边上等边三角形的面积,即$\frac{\sqrt{3}}{4}a^2 + \frac{\sqrt{3}}{4}b^2 = \frac{\sqrt{3}}{4}c^2$。
图①中3个正方形的面积关系:以a为边长的正方形面积+以b为边长的正方形面积=以c为边长的正方形面积,即$a^2 + b^2 = c^2$。
图②中3个半圆的面积关系:以a为直径的半圆面积+以b为直径的半圆面积=以c为直径的半圆面积,即$\frac{1}{2}\pi(\frac{a}{2})^2 + \frac{1}{2}\pi(\frac{b}{2})^2 = \frac{1}{2}\pi(\frac{c}{2})^2$。
(2)发现:以直角三角形三边为对应边的图形(如正方形、半圆),若这些图形的面积与对应边长的平方成正比,则两直角边上图形面积之和等于斜边上图形的面积。
设计问题:以Rt△ABC的三边为边长的3个等边三角形的面积之间有什么关系?
解答:设Rt△ABC的两条直角边为a、b,斜边为c,等边三角形面积公式为$\frac{\sqrt{3}}{4}×边长^2$。则以a、b为边长的等边三角形面积之和为$\frac{\sqrt{3}}{4}a^2 + \frac{\sqrt{3}}{4}b^2 = \frac{\sqrt{3}}{4}(a^2 + b^2)$,因为$a^2 + b^2 = c^2$,所以两直角边上等边三角形面积之和等于斜边上等边三角形的面积,即$\frac{\sqrt{3}}{4}a^2 + \frac{\sqrt{3}}{4}b^2 = \frac{\sqrt{3}}{4}c^2$。