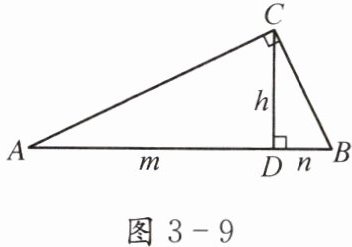
如图 3-9,CD 是 Rt△ABC 的斜边 AB 上的高,设 BC= a,AC= b,AB= c,CD= h,AD= m,DB= n.你能尝试写出这些线段之间的数量关系吗?

答案:【解析】:
本题主要考查勾股定理以及三角形面积公式的应用。
在直角三角形中,根据勾股定理,直角边的平方和等于斜边的平方,即$a^{2}+b^{2}=c^{2}$。
同时,利用三角形面积公式,可以得到$S_{\bigtriangleup ABC}=\frac{1}{2}ab=\frac{1}{2}ch$,进一步化简得到$ab=ch$。
再者,在直角三角形中,根据射影定理,有$b^{2}=mc$和$a^{2}=nc$。
最后,由于$AB=AD+DB$,所以$c=m+n$。
【答案】:
解:由勾股定理得,$a^{2}+b^{2}=c^{2}$;
由三角形面积公式得,$S_{\bigtriangleup ABC}=\frac{1}{2}ab=\frac{1}{2}ch$,即$ab=ch$;
由射影定理得,$b^{2}=mc$,$a^{2}=nc$;
且$c=m+n$。
本题主要考查勾股定理以及三角形面积公式的应用。
在直角三角形中,根据勾股定理,直角边的平方和等于斜边的平方,即$a^{2}+b^{2}=c^{2}$。
同时,利用三角形面积公式,可以得到$S_{\bigtriangleup ABC}=\frac{1}{2}ab=\frac{1}{2}ch$,进一步化简得到$ab=ch$。
再者,在直角三角形中,根据射影定理,有$b^{2}=mc$和$a^{2}=nc$。
最后,由于$AB=AD+DB$,所以$c=m+n$。
【答案】:
解:由勾股定理得,$a^{2}+b^{2}=c^{2}$;
由三角形面积公式得,$S_{\bigtriangleup ABC}=\frac{1}{2}ab=\frac{1}{2}ch$,即$ab=ch$;
由射影定理得,$b^{2}=mc$,$a^{2}=nc$;
且$c=m+n$。
例 古希腊数学家海伦在解决三角形面积计算问题时,提出了著名的海伦公式:已知三角形三边的长度a,b,c,令半周长$ p= \frac{a+b+c}{2} $,则三角形面积$ S= \sqrt{p(p-a)(p-b)(p-c)} $.大约在同一时期,中国南宋数学家秦九韶也独立推导出了类似公式——三斜求积术.秦九韶从三角形三边的长出发,运用勾股定理构造出了可以计算三角形面积的公式,与海伦公式本质相同.因此,海伦公式又被称为海伦-秦九韶公式.你能从上述描述中,运用勾股定理推导出海伦—秦九韶公式吗?
答案:解:设△ABC中,BC=a,AC=b,AB=c,过点A作AD⊥BC于点D,设BD=x,则DC=a-x,AD=h。
在Rt△ABD中,由勾股定理得:h² + x² = c² ①
在Rt△ACD中,由勾股定理得:h² + (a-x)² = b² ②
② - ①得:(a-x)² - x² = b² - c²
展开得:a² - 2ax = b² - c²
解得:x = (a² + c² - b²)/(2a)
将x代入①得:h² = c² - [(a² + c² - b²)/(2a)]²
化简得:h² = [4a²c² - (a² + c² - b²)²]/(4a²)
分子因式分解:4a²c² - (a² + c² - b²)² = (2ac + a² + c² - b²)(2ac - a² - c² + b²) = [(a+c)² - b²][b² - (a-c)²] = (a+c+b)(a+c-b)(b+a-c)(b-a+c)
设p = (a+b+c)/2,则a+c-b=2(p-b),b+a-c=2(p-c),b-a+c=2(p-a)
∴h² = [16p(p-a)(p-b)(p-c)]/(4a²) = [4p(p-a)(p-b)(p-c)]/a²
∴h = [2√(p(p-a)(p-b)(p-c))]/a
三角形面积S = (1/2)ah = (1/2)a·[2√(p(p-a)(p-b)(p-c))]/a = √(p(p-a)(p-b)(p-c))
即S = √[p(p-a)(p-b)(p-c)],其中p=(a+b+c)/2。
在Rt△ABD中,由勾股定理得:h² + x² = c² ①
在Rt△ACD中,由勾股定理得:h² + (a-x)² = b² ②
② - ①得:(a-x)² - x² = b² - c²
展开得:a² - 2ax = b² - c²
解得:x = (a² + c² - b²)/(2a)
将x代入①得:h² = c² - [(a² + c² - b²)/(2a)]²
化简得:h² = [4a²c² - (a² + c² - b²)²]/(4a²)
分子因式分解:4a²c² - (a² + c² - b²)² = (2ac + a² + c² - b²)(2ac - a² - c² + b²) = [(a+c)² - b²][b² - (a-c)²] = (a+c+b)(a+c-b)(b+a-c)(b-a+c)
设p = (a+b+c)/2,则a+c-b=2(p-b),b+a-c=2(p-c),b-a+c=2(p-a)
∴h² = [16p(p-a)(p-b)(p-c)]/(4a²) = [4p(p-a)(p-b)(p-c)]/a²
∴h = [2√(p(p-a)(p-b)(p-c))]/a
三角形面积S = (1/2)ah = (1/2)a·[2√(p(p-a)(p-b)(p-c))]/a = √(p(p-a)(p-b)(p-c))
即S = √[p(p-a)(p-b)(p-c)],其中p=(a+b+c)/2。
1. 我国南宋数学家秦九韶的著作《数书九章》中有一道问题:“问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里. 里法三百步,欲知为田几何?”问题大意:如图,在△ABC 中,AB= 13 里,BC= 14 里,AC= 15 里,则△ABC 的面积是(

A.80 平方里
B.82 平方里
C.84 平方里
D.86 平方里
C
).
A.80 平方里
B.82 平方里
C.84 平方里
D.86 平方里
答案:【解析】:本题可根据勾股定理的逆定理判断三角形的形状,再通过面积公式求解三角形的面积,也可利用海伦公式直接计算三角形面积。
方法一:利用勾股定理的逆定理和面积公式求解
步骤一:判断三角形的形状
已知在$\triangle ABC$中,$AB = 13$里,$BC = 14$里,$AC = 15$里。
过点$A$作$AD\perp BC$于点$D$,设$BD = x$里,则$CD=(14 - x)$里。
在$Rt\triangle ABD$中,根据勾股定理可得$AD^{2}=AB^{2}-BD^{2}=13^{2}-x^{2}$;
在$Rt\triangle ACD$中,根据勾股定理可得$AD^{2}=AC^{2}-CD^{2}=15^{2}-(14 - x)^{2}$。
所以$13^{2}-x^{2}=15^{2}-(14 - x)^{2}$,
即$169 - x^{2}=225-(196 - 28x + x^{2})$,
去括号得$169 - x^{2}=225 - 196 + 28x - x^{2}$,
移项可得$-x^{2}+x^{2}-28x=225 - 196 - 169$,
合并同类项得$-28x=-140$,
解得$x = 5$。
步骤二:计算$AD$的长度
把$x = 5$代入$AD^{2}=13^{2}-x^{2}$,可得$AD^{2}=13^{2}-5^{2}=169 - 25 = 144$,
因为$AD\gt0$,所以$AD = 12$里。
步骤三:计算$\triangle ABC$的面积
根据三角形面积公式$S=\frac{1}{2}×底×高$,这里底$BC = 14$里,高$AD = 12$里,
所以${S}_{\triangle ABC}=\frac{1}{2}× BC× AD=\frac{1}{2}×14×12 = 84$(平方里)。
方法二:利用海伦公式求解
海伦公式为$S = \sqrt{p(p - a)(p - b)(p - c)}$,其中$a$、$b$、$c$为三角形的三边,$p=\frac{a + b + c}{2}$为半周长。
已知$a = 14$里,$b = 15$里,$c = 13$里,则$p=\frac{14 + 15 + 13}{2}=\frac{42}{2}=21$(里)。
所以${S}_{\triangle ABC}=\sqrt{21×(21 - 14)×(21 - 15)×(21 - 13)}=\sqrt{21×7×6×8}=\sqrt{7056}=84$(平方里)。
综上,$\triangle ABC$的面积是$84$平方里,答案选C。
【答案】:C
方法一:利用勾股定理的逆定理和面积公式求解
步骤一:判断三角形的形状
已知在$\triangle ABC$中,$AB = 13$里,$BC = 14$里,$AC = 15$里。
过点$A$作$AD\perp BC$于点$D$,设$BD = x$里,则$CD=(14 - x)$里。
在$Rt\triangle ABD$中,根据勾股定理可得$AD^{2}=AB^{2}-BD^{2}=13^{2}-x^{2}$;
在$Rt\triangle ACD$中,根据勾股定理可得$AD^{2}=AC^{2}-CD^{2}=15^{2}-(14 - x)^{2}$。
所以$13^{2}-x^{2}=15^{2}-(14 - x)^{2}$,
即$169 - x^{2}=225-(196 - 28x + x^{2})$,
去括号得$169 - x^{2}=225 - 196 + 28x - x^{2}$,
移项可得$-x^{2}+x^{2}-28x=225 - 196 - 169$,
合并同类项得$-28x=-140$,
解得$x = 5$。
步骤二:计算$AD$的长度
把$x = 5$代入$AD^{2}=13^{2}-x^{2}$,可得$AD^{2}=13^{2}-5^{2}=169 - 25 = 144$,
因为$AD\gt0$,所以$AD = 12$里。
步骤三:计算$\triangle ABC$的面积
根据三角形面积公式$S=\frac{1}{2}×底×高$,这里底$BC = 14$里,高$AD = 12$里,
所以${S}_{\triangle ABC}=\frac{1}{2}× BC× AD=\frac{1}{2}×14×12 = 84$(平方里)。
方法二:利用海伦公式求解
海伦公式为$S = \sqrt{p(p - a)(p - b)(p - c)}$,其中$a$、$b$、$c$为三角形的三边,$p=\frac{a + b + c}{2}$为半周长。
已知$a = 14$里,$b = 15$里,$c = 13$里,则$p=\frac{14 + 15 + 13}{2}=\frac{42}{2}=21$(里)。
所以${S}_{\triangle ABC}=\sqrt{21×(21 - 14)×(21 - 15)×(21 - 13)}=\sqrt{21×7×6×8}=\sqrt{7056}=84$(平方里)。
综上,$\triangle ABC$的面积是$84$平方里,答案选C。
【答案】:C