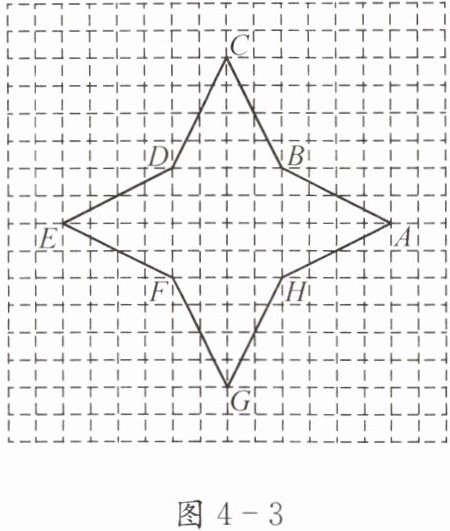
答案：解：以四角星形的中心为原点，水平方向为x轴，竖直方向为y轴建立平面直角坐标系。
顶点坐标分别为：A(5,0)，B(2,2)，C(0,5)，D(-2,2)，E(-5,0)，F(-2,-2)，G(0,-5)，H(2,-2)。

答案：【解析】：
本题主要考查平面直角坐标系的建立以及点的坐标确定。
在平面直角坐标系中，点的坐标由横坐标和纵坐标共同确定。
已知以$BC$的中点为原点，$BC$所在的直线为$x$轴建立平面直角坐标系，$BC = 6$，$AB = 3$。
先确定$B$、$C$两点的坐标：
因为$BC$的中点为原点$O$，$BC = 6$，所以$B$点在$x$轴负半轴上，且到原点的距离为$3$，则$B$点坐标为$(-3,0)$；
$C$点在$x$轴正半轴上，且到原点的距离为$3$，则$C$点坐标为$(3,0)$。
再确定$A$、$D$两点的坐标：
由于$AB$垂直于$x$轴，$AB = 3$，$B$点坐标为$(-3,0)$，那么$A$点横坐标与$B$点相同为$-3$，纵坐标为$3$，所以$A$点坐标为$(-3,3)$；
$D$点与$A$点纵坐标相同为$3$，横坐标与$C$点相同为$3$，所以$D$点坐标为$(3,3)$。
【答案】：
$A(-3,3)$，$B(-3,0)$，$C(3,0)$，$D(3,3)$

答案：【解析】：
本题考查平面直角坐标系的建立以及正方形顶点和对角线交点坐标的求解，关键在于合理建立不同的平面直角坐标系，再根据正方形的性质和坐标的定义来确定各点坐标。
【答案】：
解：(1)以点$A$为坐标原点，$AB$所在直线为$x$轴，$AD$所在直线为$y$轴建立平面直角坐标系。
因为正方形$ABCD$的边长为$2$，
所以$A(0,0)$，$B(2,0)$，$C(2,2)$，$D(0,2)$。
对角线$AC$与$BD$的交点坐标，即正方形中心坐标为$(\frac{0 + 2}{2},\frac{0 + 2}{2})=(1,1)$。
(2)以正方形$ABCD$的中心$O$为坐标原点，平行于$AB$的直线为$x$轴，平行于$AD$的直线为$y$轴建立平面直角坐标系。
此时$A(-1,-1)$，$B(1,-1)$，$C(1,1)$，$D(-1,1)$，对角线交点$O(0,0)$。