1. 填空题:
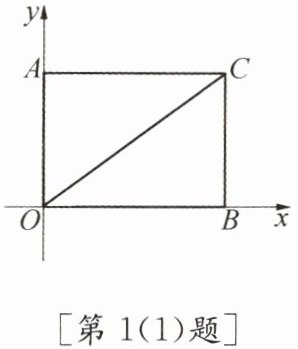
(1) 如图,在平面直角坐标系中,长方形AOBC的长为3,宽为2,则点A的坐标是

(2) 如图,正方形ABCD的边长为2,以边AB的中点O为原点,AB所在的直线为x轴建立平面直角坐标系,则点A,B,C,D的坐标分别是
(1) 如图,在平面直角坐标系中,长方形AOBC的长为3,宽为2,则点A的坐标是
(0,2)
,点B的坐标是(3,0)
,点C的坐标是(3,2)
,OC的长是$\sqrt{13}$
;

(2) 如图,正方形ABCD的边长为2,以边AB的中点O为原点,AB所在的直线为x轴建立平面直角坐标系,则点A,B,C,D的坐标分别是
(-1,0)
,(1,0)
,(1,2)
,(-1,2)
,点D在二
象限.答案:【解析】:
(1) 本题可根据长方形的性质以及平面直角坐标系的特点来确定各点坐标和线段长度。
在平面直角坐标系中,点$A$在$y$轴上,且$OA$为长方形的宽,已知长方形$AOBC$的宽为$2$,所以$OA = 2$,则点$A$的坐标是$(0,2)$。
点$B$在$x$轴上,且$OB$为长方形的长,已知长方形$AOBC$的长为$3$,所以$OB = 3$,则点$B$的坐标是$(3,0)$。
因为四边形$AOBC$是长方形,$AC$与$OB$平行且相等,$AC$在$y = 2$这条直线上,$C$点横坐标与$B$点横坐标相同为$3$,所以点$C$的坐标是$(3,2)$。
根据两点间距离公式,对于$O(0,0)$,$C(3,2)$,$OC=\sqrt{(3 - 0)^2+(2 - 0)^2}=\sqrt{9 + 4}=\sqrt{13}$,也可根据长方形性质,$OC$是长方形的对角线,由勾股定理$OC=\sqrt{3^{2}+2^{2}}=\sqrt{13}$。
(2) 本题可根据正方形的性质以及所建立的平面直角坐标系来确定各点坐标和点所在象限。
已知正方形$ABCD$的边长为$2$,以边$AB$的中点$O$为原点,$AB$所在的直线为$x$轴建立平面直角坐标系。
因为$AB = 2$,$O$是$AB$中点,所以$OA=OB = 1$,点$A$在$x$轴负半轴上,坐标为$(-1,0)$;点$B$在$x$轴正半轴上,坐标为$(1,0)$。
由于四边形$ABCD$是正方形,$AD = AB = 2$,点$D$在第二象限,$D$点横坐标与$A$点横坐标相同为$-1$,纵坐标为$2$,所以点$D$的坐标是$(-1,2)$。
$C$点横坐标与$B$点横坐标相同为$1$,纵坐标为$2$,所以点$C$的坐标是$(1,2)$。
点$D$的横坐标为负,纵坐标为正,所以点$D$在第二象限。
【答案】:
(1)$(0,2)$;$(3,0)$;$(3,2)$;$\sqrt{13}$
(2)$(-1,0)$;$(1,0)$;$(1,2)$;$(-1,2)$;二
(1) 本题可根据长方形的性质以及平面直角坐标系的特点来确定各点坐标和线段长度。
在平面直角坐标系中,点$A$在$y$轴上,且$OA$为长方形的宽,已知长方形$AOBC$的宽为$2$,所以$OA = 2$,则点$A$的坐标是$(0,2)$。
点$B$在$x$轴上,且$OB$为长方形的长,已知长方形$AOBC$的长为$3$,所以$OB = 3$,则点$B$的坐标是$(3,0)$。
因为四边形$AOBC$是长方形,$AC$与$OB$平行且相等,$AC$在$y = 2$这条直线上,$C$点横坐标与$B$点横坐标相同为$3$,所以点$C$的坐标是$(3,2)$。
根据两点间距离公式,对于$O(0,0)$,$C(3,2)$,$OC=\sqrt{(3 - 0)^2+(2 - 0)^2}=\sqrt{9 + 4}=\sqrt{13}$,也可根据长方形性质,$OC$是长方形的对角线,由勾股定理$OC=\sqrt{3^{2}+2^{2}}=\sqrt{13}$。
(2) 本题可根据正方形的性质以及所建立的平面直角坐标系来确定各点坐标和点所在象限。
已知正方形$ABCD$的边长为$2$,以边$AB$的中点$O$为原点,$AB$所在的直线为$x$轴建立平面直角坐标系。
因为$AB = 2$,$O$是$AB$中点,所以$OA=OB = 1$,点$A$在$x$轴负半轴上,坐标为$(-1,0)$;点$B$在$x$轴正半轴上,坐标为$(1,0)$。
由于四边形$ABCD$是正方形,$AD = AB = 2$,点$D$在第二象限,$D$点横坐标与$A$点横坐标相同为$-1$,纵坐标为$2$,所以点$D$的坐标是$(-1,2)$。
$C$点横坐标与$B$点横坐标相同为$1$,纵坐标为$2$,所以点$C$的坐标是$(1,2)$。
点$D$的横坐标为负,纵坐标为正,所以点$D$在第二象限。
【答案】:
(1)$(0,2)$;$(3,0)$;$(3,2)$;$\sqrt{13}$
(2)$(-1,0)$;$(1,0)$;$(1,2)$;$(-1,2)$;二
2. 南京钟山风景区部分景点分布如图所示,建立适当的平面直角坐标系,并写出各景点的坐标.


答案:解:以明孝陵所在位置为原点,水平向右为x轴正方向,竖直向上为y轴正方向,建立平面直角坐标系。
各景点坐标如下:
明孝陵:(0, 0);
紫金山天文台:(-1, 3);
中山陵:(1, 4);
灵谷寺:(5, 1);
中山植物园:(0, -2);
体育公园:(6, -3)。
各景点坐标如下:
明孝陵:(0, 0);
紫金山天文台:(-1, 3);
中山陵:(1, 4);
灵谷寺:(5, 1);
中山植物园:(0, -2);
体育公园:(6, -3)。
3. 如图,△ABC是边长为2的等边三角形,建立适当的平面直角坐标系,并写出各个顶点的坐标.


答案:解:以BC所在直线为x轴,BC的垂直平分线为y轴,建立平面直角坐标系。
∵△ABC是边长为2的等边三角形,
∴BC=2,BO=OC=1。
在Rt△ABO中,AB=2,BO=1,
由勾股定理得:AO=$\sqrt{AB^{2}-BO^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。
∴点B的坐标为(-1,0),点C的坐标为(1,0),点A的坐标为(0,$\sqrt{3}$)。
∵△ABC是边长为2的等边三角形,
∴BC=2,BO=OC=1。
在Rt△ABO中,AB=2,BO=1,
由勾股定理得:AO=$\sqrt{AB^{2}-BO^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。
∴点B的坐标为(-1,0),点C的坐标为(1,0),点A的坐标为(0,$\sqrt{3}$)。