4. 如图,在平面直角坐标系中,正方形ABCD四个顶点的坐标分别是A(2,1),B(6,1),C(6,5),D(2,5).
(1) 画出这个正方形;
(2) 若以点A为原点,AB所在直线为x轴,AD所在直线为y轴,建立新的平面直角坐标系,写出A,B,C,D四个点在新平面直角坐标系中的坐标;
(3) 已知点E在原平面直角坐标系中的坐标是(a,b),则它在新平面直角坐标系中的坐标是
(1) 画出这个正方形;
图略
(2) 若以点A为原点,AB所在直线为x轴,AD所在直线为y轴,建立新的平面直角坐标系,写出A,B,C,D四个点在新平面直角坐标系中的坐标;
A(0,0), B(4,0), C(4,4), D(0,4)
(3) 已知点E在原平面直角坐标系中的坐标是(a,b),则它在新平面直角坐标系中的坐标是
(a-2, b-1)
.答案:【解析】:
(1) 根据给出的坐标,我们可以在平面直角坐标系中描出四个点A(2,1),B(6,1),C(6,5),D(2,5),然后依次连接这四个点,就可以得到正方形ABCD,图略。
(2) 在新的平面直角坐标系中,点A成为原点,所以其坐标为(0,0)。点B在新的x轴上,且与点A的距离为4(原坐标系中B的x坐标减去A的x坐标),所以点B的坐标为(4,0)。点D在新的y轴上,且与点A的距离为4(原坐标系中D的y坐标减去A的y坐标),所以点D的坐标为(0,4)。点C既不在新的x轴上也不在新的y轴上,其x坐标为4(与点B相同),y坐标为4(与点D相同),所以点C的坐标为(4,4)。
(3) 对于点E(a,b)在原平面直角坐标系中的坐标,我们需要将其转换为新平面直角坐标系中的坐标。由于新坐标系的原点在原坐标系的点A(2,1)上,所以我们需要从原坐标中减去A点的坐标,即新坐标为$(a-2, b-1)$。
【答案】:
(1) 图略;
(2) $A(0,0), B(4,0), C(4,4), D(0,4)$;
(3) $(a-2, b-1)$。
(1) 根据给出的坐标,我们可以在平面直角坐标系中描出四个点A(2,1),B(6,1),C(6,5),D(2,5),然后依次连接这四个点,就可以得到正方形ABCD,图略。
(2) 在新的平面直角坐标系中,点A成为原点,所以其坐标为(0,0)。点B在新的x轴上,且与点A的距离为4(原坐标系中B的x坐标减去A的x坐标),所以点B的坐标为(4,0)。点D在新的y轴上,且与点A的距离为4(原坐标系中D的y坐标减去A的y坐标),所以点D的坐标为(0,4)。点C既不在新的x轴上也不在新的y轴上,其x坐标为4(与点B相同),y坐标为4(与点D相同),所以点C的坐标为(4,4)。
(3) 对于点E(a,b)在原平面直角坐标系中的坐标,我们需要将其转换为新平面直角坐标系中的坐标。由于新坐标系的原点在原坐标系的点A(2,1)上,所以我们需要从原坐标中减去A点的坐标,即新坐标为$(a-2, b-1)$。
【答案】:
(1) 图略;
(2) $A(0,0), B(4,0), C(4,4), D(0,4)$;
(3) $(a-2, b-1)$。
5. 在平面直角坐标系中,△ABC的位置如图所示,△DEF的顶点坐标分别是D(0,-1),E(-4,-3),F(-1,-3).
(1) △ABC的顶点坐标分别是
(2) 画出△DEF;
(3) 过原点O任意画一条直线l分别交BC,EF于点M,N.已知点M的坐标是(a,b),则点N的坐标是
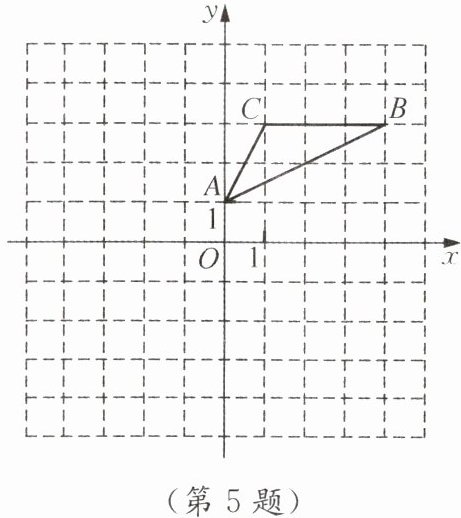
(1) △ABC的顶点坐标分别是
A(1,1)
,B(4,2)
,C(1,2)
;(2) 画出△DEF;
(3) 过原点O任意画一条直线l分别交BC,EF于点M,N.已知点M的坐标是(a,b),则点N的坐标是
(-a,-b)
.
答案:
(1) A(1,1),B(4,2),C(1,2)
(2) 图略
(3) (-a,-b)
(1) A(1,1),B(4,2),C(1,2)
(2) 图略
(3) (-a,-b)
6. 在平面直角坐标系中,点A的坐标是(0,1),点B的坐标是(4,2),是否存在点C,满足AC= BC,∠BAC= 45°?若存在,请直接写出点C的坐标;若不存在,请说明理由.
答案:解:存在点C。
设点C的坐标为(x,y)。
∵AC=BC,
∴$\sqrt{x^{2}+(y-1)^{2}}=\sqrt{(x-4)^{2}+(y-2)^{2}}$,
化简得$8x + 2y = 19$,即$y=\frac{19 - 8x}{2}$。
∵∠BAC=45°,
向量AB=(4,1),向量AC=(x,y-1),
$cos\angle BAC=\frac{AB\cdot AC}{|AB||AC|}=\frac{\sqrt{2}}{2}$,
$AB\cdot AC=4x + 1×(y - 1)=4x + y - 1$,
$|AB|=\sqrt{4^{2}+1^{2}}=\sqrt{17}$,
$|AC|=\sqrt{x^{2}+(y - 1)^{2}}$,
∴$\frac{4x + y - 1}{\sqrt{17}×\sqrt{x^{2}+(y - 1)^{2}}}=\frac{\sqrt{2}}{2}$。
将$y=\frac{19 - 8x}{2}$代入上式并化简,得$x^{2}-8x + 16=0$,
解得$x = 4$,则$y=\frac{19 - 8×4}{2}=-\frac{13}{2}$。
∴点C的坐标为$(4,-\frac{13}{2})$。
设点C的坐标为(x,y)。
∵AC=BC,
∴$\sqrt{x^{2}+(y-1)^{2}}=\sqrt{(x-4)^{2}+(y-2)^{2}}$,
化简得$8x + 2y = 19$,即$y=\frac{19 - 8x}{2}$。
∵∠BAC=45°,
向量AB=(4,1),向量AC=(x,y-1),
$cos\angle BAC=\frac{AB\cdot AC}{|AB||AC|}=\frac{\sqrt{2}}{2}$,
$AB\cdot AC=4x + 1×(y - 1)=4x + y - 1$,
$|AB|=\sqrt{4^{2}+1^{2}}=\sqrt{17}$,
$|AC|=\sqrt{x^{2}+(y - 1)^{2}}$,
∴$\frac{4x + y - 1}{\sqrt{17}×\sqrt{x^{2}+(y - 1)^{2}}}=\frac{\sqrt{2}}{2}$。
将$y=\frac{19 - 8x}{2}$代入上式并化简,得$x^{2}-8x + 16=0$,
解得$x = 4$,则$y=\frac{19 - 8×4}{2}=-\frac{13}{2}$。
∴点C的坐标为$(4,-\frac{13}{2})$。