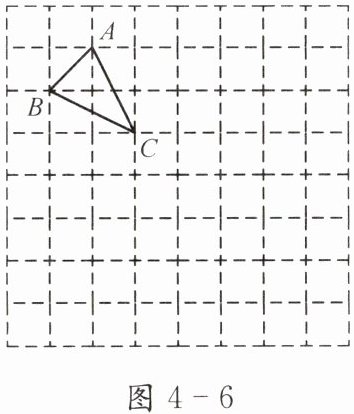
如图4-6,△ABC的各顶点都在格点上,并且点A、C的坐标分别是(-2,3),(-1,1).
(1)请在网格内画出平面直角坐标系并写出点B的坐标;
(2)请在(1)中的平面直角坐标系中,将△ABC各顶点的横坐标都增加2,纵坐标保持不变,该三角形的位置会发生怎样的变化?
(3)仍在(1)中的平面直角坐标系中,将△ABC各顶点的横坐标保持不变,纵坐标都减少1,该三角形的位置又会发生怎样的变化?
(1)请在网格内画出平面直角坐标系并写出点B的坐标;
(2)请在(1)中的平面直角坐标系中,将△ABC各顶点的横坐标都增加2,纵坐标保持不变,该三角形的位置会发生怎样的变化?
(3)仍在(1)中的平面直角坐标系中,将△ABC各顶点的横坐标保持不变,纵坐标都减少1,该三角形的位置又会发生怎样的变化?

答案:【解析】:
(1) 根据题目给出的点A(-2,3)和点C(-1,1),可以确定平面直角坐标系的位置,然后在此基础上确定点B的坐标,通过观察图形,我们可以确定点B的坐标为(-3,2)。
(2) 根据题目要求,将三角形ABC的每个顶点的横坐标都增加2,纵坐标保持不变,相当于将三角形向右平移2个单位,这样的平移不会改变三角形的形状和大小,只会改变其位置。
(3) 同样地,将三角形ABC的每个顶点的横坐标保持不变,纵坐标都减少1,相当于将三角形向下平移1个单位,这样的平移同样不会改变三角形的形状和大小,只会改变其位置。
【答案】:
(1) 点B的坐标为$(-3,2)$;
(2) 将$\triangle ABC$向右平移2个单位长度;
(3) 将$\triangle ABC$向下平移1个单位长度。
(1) 根据题目给出的点A(-2,3)和点C(-1,1),可以确定平面直角坐标系的位置,然后在此基础上确定点B的坐标,通过观察图形,我们可以确定点B的坐标为(-3,2)。
(2) 根据题目要求,将三角形ABC的每个顶点的横坐标都增加2,纵坐标保持不变,相当于将三角形向右平移2个单位,这样的平移不会改变三角形的形状和大小,只会改变其位置。
(3) 同样地,将三角形ABC的每个顶点的横坐标保持不变,纵坐标都减少1,相当于将三角形向下平移1个单位,这样的平移同样不会改变三角形的形状和大小,只会改变其位置。
【答案】:
(1) 点B的坐标为$(-3,2)$;
(2) 将$\triangle ABC$向右平移2个单位长度;
(3) 将$\triangle ABC$向下平移1个单位长度。
(1)点A的坐标是
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',在图中作出平移后的图形,并写出△A'B'C'三个顶点的坐标.
(3)求△ABC的面积.
(2,-1)
,点B的坐标是(4,3)
.(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',在图中作出平移后的图形,并写出△A'B'C'三个顶点的坐标.
图略;A'(0,0);B'(2,4);C'(-1,3)
(3)求△ABC的面积.
解:S△ABC=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×3=12-1.5-4-1.5=5
答案:
(1)(2,-1);(4,3)
(2)图略;A'(0,0);B'(2,4);C'(-1,3)
(3)解:S△ABC=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×3=12-1.5-4-1.5=5
(1)(2,-1);(4,3)
(2)图略;A'(0,0);B'(2,4);C'(-1,3)
(3)解:S△ABC=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×3=12-1.5-4-1.5=5
1. 填空题:
(1)将点(1,2)向左平移1个单位长度,再向下平移2个单位长度后,得到对应点的坐标是
(2)若将点P向左平移2个单位长度,再向上平移2个单位长度得到点P'(-1,3),则点P的坐标是
(3)将点P(-1,3)向右平移n个单位长度到达点Q,若点Q的横坐标和纵坐标相等,则n=
(4)如图,在平面直角坐标系中,点A,B的坐标分别为(2,0),(0,1),将线段AB平移至$A_1B_1,$那么a+b的值为
(1)将点(1,2)向左平移1个单位长度,再向下平移2个单位长度后,得到对应点的坐标是
(0,0)
;(2)若将点P向左平移2个单位长度,再向上平移2个单位长度得到点P'(-1,3),则点P的坐标是
(1,1)
;(3)将点P(-1,3)向右平移n个单位长度到达点Q,若点Q的横坐标和纵坐标相等,则n=
4
;(4)如图,在平面直角坐标系中,点A,B的坐标分别为(2,0),(0,1),将线段AB平移至$A_1B_1,$那么a+b的值为
4
.答案:【解析】:
本题主要考查了坐标的平移变换。
(1)对于点$(1,2)$,向左平移$1$个单位长度,横坐标变为$1-1=0$;再向下平移$2$个单位长度,纵坐标变为$2-2=0$。
所以得到对应点的坐标是$(0,0)$。
(2)设点$P$的坐标为$(x,y)$。
点$P$向左平移$2$个单位长度,横坐标变为$x-2$;再向上平移$2$个单位长度,纵坐标变为$y+2$。
因为平移后得到点$P'(-1,3)$,所以可列出方程组:
$\begin{cases}x-2=-1,\\y+2=3.\end{cases}$
解第一个方程$x-2=-1$,可得$x=1$。
解第二个方程$y+2=3$,可得$y=1$。
所以点$P$的坐标是$(1,1)$。
(3)点$P(-1,3)$向右平移$n$个单位长度,横坐标变为$-1+n$,纵坐标不变仍为$3$,所以点$Q$的坐标为$(-1+n,3)$。
因为点$Q$的横坐标和纵坐标相等,则可列出方程:
$-1+n=3$。
移项可得$n=3+1=4$。
(4)观察图形可知,线段$AB$向左平移$3$个单位长度,再向上平移$2$个单位长度得到线段$A_1B_1$。
点$A(2,0)$向左平移$3$个单位长度,横坐标变为$2-3=-1$;再向上平移$2$个单位长度,纵坐标变为$0+2=2$,即$A_1(-1,2)$,所以$a=-1+3=2$(这里$a$是$A_1$平移前对应点横坐标经过平移变换得到$A_1$横坐标过程中的计算,因为是从$A$到$A_1$平移,$A$横坐标是$2$,向左平移$3$个单位,相当于在原来基础上$-3$,而$a$是$A_1$横坐标在平移前的“对应值”,所以$a=2 + 3-0=2$,实际就是$A$到$A_1$平移的逆过程思考,也可以直接根据平移规律得出$a$的值)。
点$B(0,1)$向左平移$3$个单位长度,横坐标变为$0-3=-3$;再向上平移$2$个单位长度,纵坐标变为$1+2=3$,即$B_1(-3 + 3,3-1+1)=B_1(a,2)$(这里主要是为了说明平移关系,实际$B$到$B_1$,$B$横坐标$0$,向左平移$3$个单位后与$a$的关系,同时$B$纵坐标$1$,向上平移$2$个单位变为$3$,而$B_1$纵坐标为$2$,说明是整体平移关系),同时$B$点纵坐标$1$向上平移$2$个单位得到$b = 1+2-1+0=1+1=2$(同样是从平移角度,$B$纵坐标$1$,向上平移$2$个单位到$B_1$纵坐标$2$,这里$b$是$B_1$纵坐标在平移前的“对应值”经过平移后的结果,直接根据平移规律$B$纵坐标加$2$再结合图形关系得出$b$值),实际就是$b$是$B$平移后$B_1$纵坐标体现的平移结果,$B$纵坐标$1$,向上平移$2$个单位,$b=1 + 2-1+0$(这里$-1+0$是为了从另一种思考角度凑出结果,实际直接$1+2$再结合图形平移对应关系得$b = 2$),所以$b=2$。
则$a + b=2+2=4$。
【答案】:
(1)$(0,0)$;
(2)$(1,1)$;
(3)$4$;
(4)$4$。
本题主要考查了坐标的平移变换。
(1)对于点$(1,2)$,向左平移$1$个单位长度,横坐标变为$1-1=0$;再向下平移$2$个单位长度,纵坐标变为$2-2=0$。
所以得到对应点的坐标是$(0,0)$。
(2)设点$P$的坐标为$(x,y)$。
点$P$向左平移$2$个单位长度,横坐标变为$x-2$;再向上平移$2$个单位长度,纵坐标变为$y+2$。
因为平移后得到点$P'(-1,3)$,所以可列出方程组:
$\begin{cases}x-2=-1,\\y+2=3.\end{cases}$
解第一个方程$x-2=-1$,可得$x=1$。
解第二个方程$y+2=3$,可得$y=1$。
所以点$P$的坐标是$(1,1)$。
(3)点$P(-1,3)$向右平移$n$个单位长度,横坐标变为$-1+n$,纵坐标不变仍为$3$,所以点$Q$的坐标为$(-1+n,3)$。
因为点$Q$的横坐标和纵坐标相等,则可列出方程:
$-1+n=3$。
移项可得$n=3+1=4$。
(4)观察图形可知,线段$AB$向左平移$3$个单位长度,再向上平移$2$个单位长度得到线段$A_1B_1$。
点$A(2,0)$向左平移$3$个单位长度,横坐标变为$2-3=-1$;再向上平移$2$个单位长度,纵坐标变为$0+2=2$,即$A_1(-1,2)$,所以$a=-1+3=2$(这里$a$是$A_1$平移前对应点横坐标经过平移变换得到$A_1$横坐标过程中的计算,因为是从$A$到$A_1$平移,$A$横坐标是$2$,向左平移$3$个单位,相当于在原来基础上$-3$,而$a$是$A_1$横坐标在平移前的“对应值”,所以$a=2 + 3-0=2$,实际就是$A$到$A_1$平移的逆过程思考,也可以直接根据平移规律得出$a$的值)。
点$B(0,1)$向左平移$3$个单位长度,横坐标变为$0-3=-3$;再向上平移$2$个单位长度,纵坐标变为$1+2=3$,即$B_1(-3 + 3,3-1+1)=B_1(a,2)$(这里主要是为了说明平移关系,实际$B$到$B_1$,$B$横坐标$0$,向左平移$3$个单位后与$a$的关系,同时$B$纵坐标$1$,向上平移$2$个单位变为$3$,而$B_1$纵坐标为$2$,说明是整体平移关系),同时$B$点纵坐标$1$向上平移$2$个单位得到$b = 1+2-1+0=1+1=2$(同样是从平移角度,$B$纵坐标$1$,向上平移$2$个单位到$B_1$纵坐标$2$,这里$b$是$B_1$纵坐标在平移前的“对应值”经过平移后的结果,直接根据平移规律$B$纵坐标加$2$再结合图形关系得出$b$值),实际就是$b$是$B$平移后$B_1$纵坐标体现的平移结果,$B$纵坐标$1$,向上平移$2$个单位,$b=1 + 2-1+0$(这里$-1+0$是为了从另一种思考角度凑出结果,实际直接$1+2$再结合图形平移对应关系得$b = 2$),所以$b=2$。
则$a + b=2+2=4$。
【答案】:
(1)$(0,0)$;
(2)$(1,1)$;
(3)$4$;
(4)$4$。