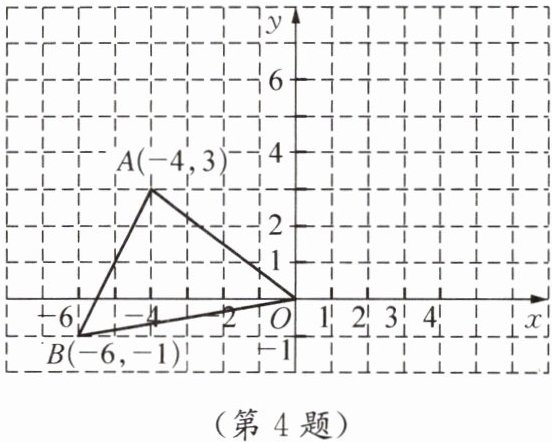
4. 如图,把△ABO向上平移3个单位长度,得到$△A_1B_1O_1;$把△ABO沿y轴翻折,得到$△A_2B_2O_2;$把△ABO绕点O按顺时针方向旋转90°,得到$△A_3B_3O_3.$
(1)已知点A,B,O的坐标分别为(-4,3),(-6,-1),(0,0),分别写出点$A_1,B_1,O_1,A_2,B_2,O_2,A_3,B_3,O_3$的坐标;
(2)如果P(x₀,y₀)为△ABO中任意一点,经上述平移、翻折、旋转后分别得到点$P_1,P_2,P_3,$写出点$P_1,P_2,P_3$的坐标.
(1)已知点A,B,O的坐标分别为(-4,3),(-6,-1),(0,0),分别写出点$A_1,B_1,O_1,A_2,B_2,O_2,A_3,B_3,O_3$的坐标;
(2)如果P(x₀,y₀)为△ABO中任意一点,经上述平移、翻折、旋转后分别得到点$P_1,P_2,P_3,$写出点$P_1,P_2,P_3$的坐标.

答案:【解析】:
本题主要考查图形的平移、翻折和旋转在坐标系中的变换规则。
(1)对于平移变换,向上平移3个单位长度,纵坐标加3,横坐标不变。
对于沿y轴翻折,横坐标变为相反数,纵坐标不变。
对于绕点O按顺时针方向旋转$90^\circ$,根据旋转矩阵$\begin{bmatrix}0&1\\-1&0\end{bmatrix}$,
即$(x,y)$变为$(y,-x)$。
已知点$A(-4,3)$,$B(-6,-1)$,$O(0,0)$。
点$A_1$的坐标:$A_1(-4,3+3)=(-4,6)$。
点$B_1$的坐标:$B_1(-6,-1+3)=(-6,2)$。
点$O_1$的坐标:$O_1(0,0+3)=(0,3)$。
点$A_2$的坐标:$A_2(-(-4),3)=(4,3)$。
点$B_2$的坐标:$B_2(-(-6),-1)=(6,-1)$。
点$O_2$的坐标:$O_2(0,0)$(翻折不改变原点坐标)。
点$A_3$的坐标:$A_3(3,4)$(绕O点旋转$90^\circ$)。
点$B_3$的坐标:$B_3(-1,6)$(绕O点旋转$90^\circ$)。
点$O_3$的坐标:$O_3(0,0)$(旋转不改变原点坐标)。
(2)对于点$P(x_0,y_0)$,经过上述变换后:
点$P_1$的坐标:$P_1(x_0,y_0+3)$(平移)。
点$P_2$的坐标:$P_2(-x_0,y_0)$(翻折)。
点$P_3$的坐标:$P_3(y_0,-x_0)$(旋转)。
【答案】:
(1)$A_1(-4,6)$;$B_1(-6,2)$;$O_1(0,3)$;$A_2(4,3)$;$B_2(6,-1)$;$O_2(0,0)$;$A_3(3,4)$;$B_3(-1,6)$;$O_3(0,0)$。
(2)$P_1(x_0,y_0+3)$;$P_2(-x_0,y_0)$;$P_3(y_0,-x_0)$。
本题主要考查图形的平移、翻折和旋转在坐标系中的变换规则。
(1)对于平移变换,向上平移3个单位长度,纵坐标加3,横坐标不变。
对于沿y轴翻折,横坐标变为相反数,纵坐标不变。
对于绕点O按顺时针方向旋转$90^\circ$,根据旋转矩阵$\begin{bmatrix}0&1\\-1&0\end{bmatrix}$,
即$(x,y)$变为$(y,-x)$。
已知点$A(-4,3)$,$B(-6,-1)$,$O(0,0)$。
点$A_1$的坐标:$A_1(-4,3+3)=(-4,6)$。
点$B_1$的坐标:$B_1(-6,-1+3)=(-6,2)$。
点$O_1$的坐标:$O_1(0,0+3)=(0,3)$。
点$A_2$的坐标:$A_2(-(-4),3)=(4,3)$。
点$B_2$的坐标:$B_2(-(-6),-1)=(6,-1)$。
点$O_2$的坐标:$O_2(0,0)$(翻折不改变原点坐标)。
点$A_3$的坐标:$A_3(3,4)$(绕O点旋转$90^\circ$)。
点$B_3$的坐标:$B_3(-1,6)$(绕O点旋转$90^\circ$)。
点$O_3$的坐标:$O_3(0,0)$(旋转不改变原点坐标)。
(2)对于点$P(x_0,y_0)$,经过上述变换后:
点$P_1$的坐标:$P_1(x_0,y_0+3)$(平移)。
点$P_2$的坐标:$P_2(-x_0,y_0)$(翻折)。
点$P_3$的坐标:$P_3(y_0,-x_0)$(旋转)。
【答案】:
(1)$A_1(-4,6)$;$B_1(-6,2)$;$O_1(0,3)$;$A_2(4,3)$;$B_2(6,-1)$;$O_2(0,0)$;$A_3(3,4)$;$B_3(-1,6)$;$O_3(0,0)$。
(2)$P_1(x_0,y_0+3)$;$P_2(-x_0,y_0)$;$P_3(y_0,-x_0)$。
5. 点A在平面直角坐标系中的位置如图所示,直线l经过点B(-3,0)且平行于y轴.
(1)写出点A关于y轴的对称点$A_1$的坐标
(2)若平面直角坐标系中有一点P(m,n),其中m>0,点P关于y轴的对称点为$P_1,$点$P_1$关于直线l的对称点为$P_2,$求线段$P_1P_2$的长(用含m的式子表示).

(2)解:∵点P(m,n),m>0
∴点P关于y轴的对称点P₁(-m,n)
∵直线l经过点B(-3,0)且平行于y轴
∴直线l为x=-3
设点P₁(-m,n)关于直线l的对称点P₂(x,n)
则$\frac{-m + x}{2}=-3$
解得x=-6 + m
∴P₂(m - 6,n)
∴P₁P₂=|m - 6 - (-m)|=|2m - 6|
∵m>0,当m>0时,2m - 6可能为正也可能为负,但线段长度为正值,由对称性质可知m - 6<-m(m>0),所以P₁P₂= - (m - 6) + m = 6 - 2m(或直接由计算得|2m - 6|,因m>0,当m<3时为6 - 2m,当m≥3时为2m - 6,但根据图形对称关系及P₁在直线l左侧,P₂在直线l左侧或右侧,综合可知此处应为6 - 2m)
即线段P₁P₂的长为6 - 2m
(1)写出点A关于y轴的对称点$A_1$的坐标
(-2,3)
,点A关于直线l的对称点$A_2$的坐标(-4,3)
;(2)若平面直角坐标系中有一点P(m,n),其中m>0,点P关于y轴的对称点为$P_1,$点$P_1$关于直线l的对称点为$P_2,$求线段$P_1P_2$的长(用含m的式子表示).

(2)解:∵点P(m,n),m>0
∴点P关于y轴的对称点P₁(-m,n)
∵直线l经过点B(-3,0)且平行于y轴
∴直线l为x=-3
设点P₁(-m,n)关于直线l的对称点P₂(x,n)
则$\frac{-m + x}{2}=-3$
解得x=-6 + m
∴P₂(m - 6,n)
∴P₁P₂=|m - 6 - (-m)|=|2m - 6|
∵m>0,当m>0时,2m - 6可能为正也可能为负,但线段长度为正值,由对称性质可知m - 6<-m(m>0),所以P₁P₂= - (m - 6) + m = 6 - 2m(或直接由计算得|2m - 6|,因m>0,当m<3时为6 - 2m,当m≥3时为2m - 6,但根据图形对称关系及P₁在直线l左侧,P₂在直线l左侧或右侧,综合可知此处应为6 - 2m)
即线段P₁P₂的长为6 - 2m
答案:(1)(-2,3); (-4,3)
(2)解:∵点P(m,n),m>0
∴点P关于y轴的对称点P₁(-m,n)
∵直线l经过点B(-3,0)且平行于y轴
∴直线l为x=-3
设点P₁(-m,n)关于直线l的对称点P₂(x,n)
则$\frac{-m + x}{2}=-3$
解得x=-6 + m
∴P₂(m - 6,n)
∴P₁P₂=|m - 6 - (-m)|=|2m - 6|
∵m>0,当m>0时,2m - 6可能为正也可能为负,但线段长度为正值,由对称性质可知m - 6<-m(m>0),所以P₁P₂= - (m - 6) + m = 6 - 2m(或直接由计算得|2m - 6|,因m>0,当m<3时为6 - 2m,当m≥3时为2m - 6,但根据图形对称关系及P₁在直线l左侧,P₂在直线l左侧或右侧,综合可知此处应为6 - 2m)
即线段P₁P₂的长为6 - 2m
(2)解:∵点P(m,n),m>0
∴点P关于y轴的对称点P₁(-m,n)
∵直线l经过点B(-3,0)且平行于y轴
∴直线l为x=-3
设点P₁(-m,n)关于直线l的对称点P₂(x,n)
则$\frac{-m + x}{2}=-3$
解得x=-6 + m
∴P₂(m - 6,n)
∴P₁P₂=|m - 6 - (-m)|=|2m - 6|
∵m>0,当m>0时,2m - 6可能为正也可能为负,但线段长度为正值,由对称性质可知m - 6<-m(m>0),所以P₁P₂= - (m - 6) + m = 6 - 2m(或直接由计算得|2m - 6|,因m>0,当m<3时为6 - 2m,当m≥3时为2m - 6,但根据图形对称关系及P₁在直线l左侧,P₂在直线l左侧或右侧,综合可知此处应为6 - 2m)
即线段P₁P₂的长为6 - 2m