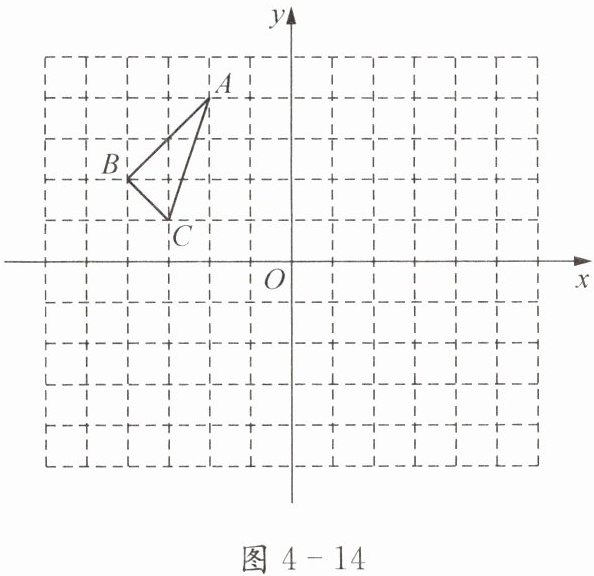
例3 △ABC在平面直角坐标系中的位置如图4-14所示,其中每个小正方形的边长为1个单位长度.
(1)将△ABC向右平移2个单位长度,画出平移后的$△A_1B_1C_1,$并写出$△A_1B_1C_1$各顶点的坐标.
(2)将△ABC绕点(-1,0)按顺时针方向旋转180°,画出旋转后的$△A_2B_2C_2,$并写出$△A_2B_2C_2$各顶点的坐标.
(3)观察$△A_1B_1C_1$和$△A_2B_2C_2,$它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.

1. 选择题:
(1)下列说法中,能确定物体位置的是().
A. 东经110°、北纬20°
B. 离小明家5 km的大楼
C. 电影院中20座
D. 北偏西55°方向
(2)平面直角坐标系的第三象限内有一点P,到x轴的距离是3,到y轴的距离是2,则点P的坐标为().
A. (-3,2)
B. (-2,3)
C. (-3,-2)
D. (-2,-3)
(3)在平面直角坐标系中,点$ P\left(m-1,\frac{1+m}{2}\right) $在第二象限,则m的取值范围是().
A. m＜1
B. m＞-1
C. -1＜m＜1
D. -1≤m≤1
(4)如图是象棋棋盘的一部分,如果用(1,-2)表示"帥"的位置,那么点(-2,1)上的棋子是().
A. "相"
B. "馬"
C. "炮"
D. "兵"

(5)已知在平面直角坐标系中,点A,B的坐标分别是(1,0),(0,3),将线段AB平移,平移后点A的对应点A'的坐标是(-1,-1),那么点B的对应点B'的坐标是().
A. (-1,2)
B. (-2,2)
C. (-2,-2)
D. (1,2)
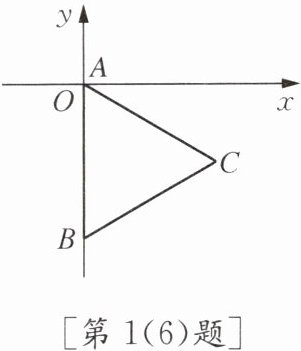
(6)如图,已知△ABC是等边三角形,边长为2,则点C的坐标是().
A. (2,-1)
B. (2,1)
C. ($\sqrt{3}$,-1)
D. (-1,$\sqrt{3}$)