1. 填空题:
(1) 按如图所示的运算程序输入一个实数x,便可以输出一个相应的y,y关于x的函数表达式是
(2) 如图,在△ABC中,∠C= 90°.① 已知∠A= 30°,则∠B=
(1) 按如图所示的运算程序输入一个实数x,便可以输出一个相应的y,y关于x的函数表达式是
y = 7x - 21
,已知输出的值为-28,那么输入的数值是-1
.(2) 如图,在△ABC中,∠C= 90°.① 已知∠A= 30°,则∠B=
60°
;② 用x°表示∠A的度数,用y°表示∠B的度数,则y= 90° - x°
,其中,自变量x的取值范围是0 < x < 90
.答案:【解析】:
(1) 题目要求根据运算程序输入一个实数 $x$,输出相应的 $y$。
运算程序为:输入 $x$ 后,先减去3,再乘以7,得到 $y$。
因此,$y$ 关于 $x$ 的函数表达式为:
$y = 7(x - 3)=7x-21$。
已知输出的 $y$ 值为 -28,那么可以列出方程:
$7(x - 3) = -28$。
解这个方程:
$7x - 21 = -28$。
$7x = -28 + 21$。
$7x = -7$。
$x = -1$。
(2)
① 在 $\triangle ABC$ 中,$\angle C = 90^\circ$,$\angle A = 30^\circ$。
根据三角形内角和为 $180^\circ$,有:
$\angle B = 180^\circ - \angle A - \angle C = 180^\circ - 30^\circ - 90^\circ = 60^\circ$。
② 用 $x^\circ$ 表示 $\angle A$ 的度数,用 $y^\circ$ 表示 $\angle B$ 的度数。
根据三角形内角和为 $180^\circ$,有:
$y = 180^\circ - x^\circ - 90^\circ = 90^\circ - x^\circ$。
其中,自变量 $x$ 的取值范围是 $0 < x < 90$,因为 $\angle A$ 和 $\angle B$ 都必须是锐角。
【答案】:
(1) $y = 7x - 21$;$-1$。
(2) $60^\circ$;$90^\circ - x^\circ$;$0 < x < 90$。
(1) 题目要求根据运算程序输入一个实数 $x$,输出相应的 $y$。
运算程序为:输入 $x$ 后,先减去3,再乘以7,得到 $y$。
因此,$y$ 关于 $x$ 的函数表达式为:
$y = 7(x - 3)=7x-21$。
已知输出的 $y$ 值为 -28,那么可以列出方程:
$7(x - 3) = -28$。
解这个方程:
$7x - 21 = -28$。
$7x = -28 + 21$。
$7x = -7$。
$x = -1$。
(2)
① 在 $\triangle ABC$ 中,$\angle C = 90^\circ$,$\angle A = 30^\circ$。
根据三角形内角和为 $180^\circ$,有:
$\angle B = 180^\circ - \angle A - \angle C = 180^\circ - 30^\circ - 90^\circ = 60^\circ$。
② 用 $x^\circ$ 表示 $\angle A$ 的度数,用 $y^\circ$ 表示 $\angle B$ 的度数。
根据三角形内角和为 $180^\circ$,有:
$y = 180^\circ - x^\circ - 90^\circ = 90^\circ - x^\circ$。
其中,自变量 $x$ 的取值范围是 $0 < x < 90$,因为 $\angle A$ 和 $\angle B$ 都必须是锐角。
【答案】:
(1) $y = 7x - 21$;$-1$。
(2) $60^\circ$;$90^\circ - x^\circ$;$0 < x < 90$。
2. 写出下列问题中的函数表达式及自变量的取值范围:
(1) 某市的民用电费标准为0.52元/(kW·h),求电费y元关于用电量x kW·h的函数表达式;
(2) 已知一等腰三角形的面积为$20 cm^2.$设它的底边长为x cm,求底边上的高y cm关于x的函数表达式.
(1) 某市的民用电费标准为0.52元/(kW·h),求电费y元关于用电量x kW·h的函数表达式;
(2) 已知一等腰三角形的面积为$20 cm^2.$设它的底边长为x cm,求底边上的高y cm关于x的函数表达式.
答案:【解析】:
本题主要考察一次函数和反比例函数的建立。
对于第一个问题,根据电费的计算方式,电费是用电量与每单位电价的乘积,可以得到电费与用电量的关系为正比例关系,利用公式$费用=单价×数量$可以得到函数表达式。自变量x代表用电量,它应该是一个非负数,因为用电量不能为负。
对于第二个问题,知道三角形的面积公式为$面积 =\frac{1}{2} × 底 × 高$,由此可以解出高y关于底边x的表达式。因为底边长是正数,且高也应该是正数,所以自变量x的取值范围是所有正实数。
【答案】:
(1)解:根据电费的计算方式,电费y与用电量x的关系可以表示为:
$y = 0.52x$
自变量x的取值范围是$x \geq 0$。
(2)解:由三角形面积公式,我们有:
$面积= \frac{1}{2}xy$
给定面积为$20cm^2$,解出y得:
$y = \frac{40}{x}$
自变量x的取值范围是$x > 0$。
本题主要考察一次函数和反比例函数的建立。
对于第一个问题,根据电费的计算方式,电费是用电量与每单位电价的乘积,可以得到电费与用电量的关系为正比例关系,利用公式$费用=单价×数量$可以得到函数表达式。自变量x代表用电量,它应该是一个非负数,因为用电量不能为负。
对于第二个问题,知道三角形的面积公式为$面积 =\frac{1}{2} × 底 × 高$,由此可以解出高y关于底边x的表达式。因为底边长是正数,且高也应该是正数,所以自变量x的取值范围是所有正实数。
【答案】:
(1)解:根据电费的计算方式,电费y与用电量x的关系可以表示为:
$y = 0.52x$
自变量x的取值范围是$x \geq 0$。
(2)解:由三角形面积公式,我们有:
$面积= \frac{1}{2}xy$
给定面积为$20cm^2$,解出y得:
$y = \frac{40}{x}$
自变量x的取值范围是$x > 0$。
3. 一支20 cm长的蜡烛点燃后,每小时燃烧5 cm.在下图中,哪幅图象能大致刻画出这支蜡烛点燃后剩下的长度h cm与点燃时间t h之间的函数关系?请说明理由.
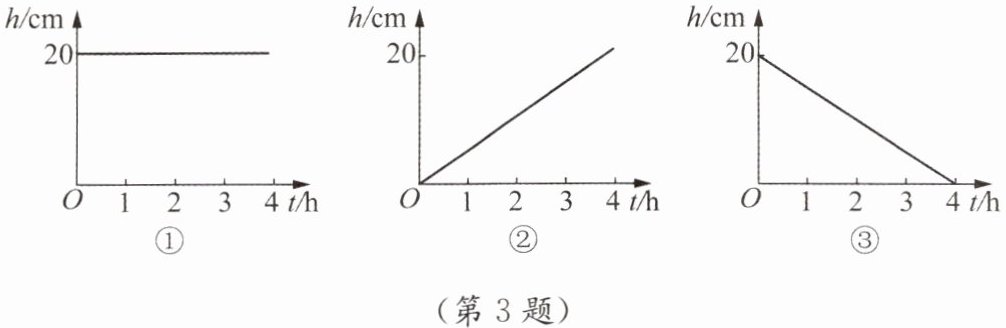
(第3题)

(第3题)
答案:【解析】:
首先分析蜡烛的燃烧情况,蜡烛初始长度为$20cm$,每小时燃烧$5cm$,那么点燃时间$t$小时后,蜡烛剩下的长度$h = 20 - 5t$。
这是一个一次函数,其中$k=-5\lt0$,$b = 20$。
接着确定函数的定义域,因为蜡烛长度不能为负,当$h = 0$时,$0=20 - 5t$,解得$t = 4$,所以$t$的取值范围是$0\leq t\leq4$。
然后分析函数图象的特征,当$t = 0$时,$h = 20$,即图象过点$(0,20)$;由于$k=-5\lt0$,$h$随$t$的增大而减小;当$t = 4$时,$h = 0$。
最后逐一分析选项,图①中$h$的值不随$t$的变化而变化,不符合蜡烛燃烧长度随时间变化的情况;图②中$h$随$t$的增大而增大,不符合$k\lt0$的情况;图③中,当$t = 0$时,$h = 20$,且$h$随$t$的增大而减小,当$t = 4$时,$h = 0$,符合蜡烛燃烧后剩下长度$h$与点燃时间$t$之间的函数关系。
【答案】:图③。理由:蜡烛剩余长度$h$与点燃时间$t$之间的函数关系为$h = 20 - 5t(0\leq t\leq4)$,$h$随$t$的增大而减小,当$t = 0$时,$h = 20$,当$t = 4$时,$h = 0$,图③符合这一关系。
首先分析蜡烛的燃烧情况,蜡烛初始长度为$20cm$,每小时燃烧$5cm$,那么点燃时间$t$小时后,蜡烛剩下的长度$h = 20 - 5t$。
这是一个一次函数,其中$k=-5\lt0$,$b = 20$。
接着确定函数的定义域,因为蜡烛长度不能为负,当$h = 0$时,$0=20 - 5t$,解得$t = 4$,所以$t$的取值范围是$0\leq t\leq4$。
然后分析函数图象的特征,当$t = 0$时,$h = 20$,即图象过点$(0,20)$;由于$k=-5\lt0$,$h$随$t$的增大而减小;当$t = 4$时,$h = 0$。
最后逐一分析选项,图①中$h$的值不随$t$的变化而变化,不符合蜡烛燃烧长度随时间变化的情况;图②中$h$随$t$的增大而增大,不符合$k\lt0$的情况;图③中,当$t = 0$时,$h = 20$,且$h$随$t$的增大而减小,当$t = 4$时,$h = 0$,符合蜡烛燃烧后剩下长度$h$与点燃时间$t$之间的函数关系。
【答案】:图③。理由:蜡烛剩余长度$h$与点燃时间$t$之间的函数关系为$h = 20 - 5t(0\leq t\leq4)$,$h$随$t$的增大而减小,当$t = 0$时,$h = 20$,当$t = 4$时,$h = 0$,图③符合这一关系。