14. 已知函数$y_{1}= x+3与函数y_{2}= -x+b$($b$为常数).
(1) 当$b= 1$时,若$y_{1}\lt y_{2}$,求$x$的取值范围;
(2) 当$x<2$时,$y_{1}\lt y_{2}$,结合图象,直接写出$b$的取值范围.
(1) 当$b= 1$时,若$y_{1}\lt y_{2}$,求$x$的取值范围;
(2) 当$x<2$时,$y_{1}\lt y_{2}$,结合图象,直接写出$b$的取值范围.
答案:(1)解:当$b = 1$时,$y_{2}=-x + 1$。
因为$y_{1}\lt y_{2}$,所以$x+3\lt -x + 1$。
移项得:$x+x\lt1 - 3$,
合并同类项得:$2x\lt - 2$,
系数化为1得:$x\lt - 1$。
(2)$b\geq5$
因为$y_{1}\lt y_{2}$,所以$x+3\lt -x + 1$。
移项得:$x+x\lt1 - 3$,
合并同类项得:$2x\lt - 2$,
系数化为1得:$x\lt - 1$。
(2)$b\geq5$
15. 某块试验田的农作物每天的需水量$y\ kg关于生长时间x$天的关系如图所示.这些农作物在第10天、第30天的需水量分别为2000kg,3000kg,在第40天后每天的需水量比前一天增加100kg.
(1) 分别求出$x<40和x\geqslant40$时,$y关于x$的函数表达式;
(2) 如果这些农作物每天的需水量大于或等于4000kg时,就需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
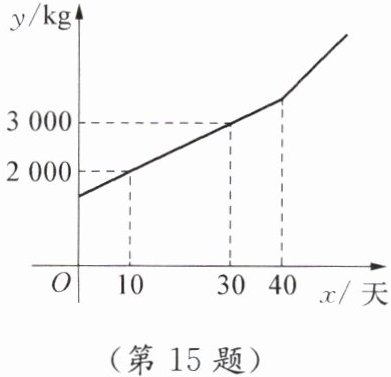
(1) 分别求出$x<40和x\geqslant40$时,$y关于x$的函数表达式;
(2) 如果这些农作物每天的需水量大于或等于4000kg时,就需要进行人工灌溉,那么应从第几天开始进行人工灌溉?

答案:(1) 当$x < 40$时,设$y = kx + b$,将$(10, 2000)$,$(30, 3000)$代入得:
$\begin{cases}10k + b = 2000 \\30k + b = 3000\end{cases}$
解得$k = 50$,$b = 1500$,$\therefore y = 50x + 1500$。
当$x = 40$时,$y = 50×40 + 1500 = 3500$。
当$x \geq 40$时,设$y = mx + n$,$m = 100$,将$(40, 3500)$代入得:
$40×100 + n = 3500$,解得$n = -500$,$\therefore y = 100x - 500$。
(2) 令$100x - 500 \geq 4000$,解得$x \geq 45$。
答:(1)$x < 40$时,$y = 50x + 1500$;$x \geq 40$时,$y = 100x - 500$。(2)应从第45天开始人工灌溉。
$\begin{cases}10k + b = 2000 \\30k + b = 3000\end{cases}$
解得$k = 50$,$b = 1500$,$\therefore y = 50x + 1500$。
当$x = 40$时,$y = 50×40 + 1500 = 3500$。
当$x \geq 40$时,设$y = mx + n$,$m = 100$,将$(40, 3500)$代入得:
$40×100 + n = 3500$,解得$n = -500$,$\therefore y = 100x - 500$。
(2) 令$100x - 500 \geq 4000$,解得$x \geq 45$。
答:(1)$x < 40$时,$y = 50x + 1500$;$x \geq 40$时,$y = 100x - 500$。(2)应从第45天开始人工灌溉。
16. 一列货车从A地出发,以100km/h的速度匀速驶往B地.若干时间后,一列客车从B地出发沿同一路线匀速驶往A地.货车行驶1.8h后,在距B地120km处与客车相遇.图中线段表示货车离B地的距离$y_{1}\ km与所用时间x\ h$的关系.根据函数的图象探究:
(1) 求$y_{1}关于x$的函数表达式;
(2) 若两车同时到达各自目的地,在同一平面直角坐标系中画出客车离B地的距离$y_{2}\ km与所用时间x\ h$的函数关系的图象,并用文字说明该图象与$x$轴的交点所表示的实际意义.

(1) 求$y_{1}关于x$的函数表达式;
(2) 若两车同时到达各自目的地,在同一平面直角坐标系中画出客车离B地的距离$y_{2}\ km与所用时间x\ h$的函数关系的图象,并用文字说明该图象与$x$轴的交点所表示的实际意义.

答案:(1)解:设$y_{1}=kx+b$。
货车速度为$100km/h$,行驶$1.8h$的路程为$100×1.8 = 180km$,此时距$B$地$120km$,则$A$、$B$两地距离为$180 + 120 = 300km$,即当$x = 0$时,$y_{1}=300$,所以$b = 300$。
又因为当$x = 1.8$时,$y_{1}=120$,代入得$1.8k + 300 = 120$,解得$k=-100$。
所以$y_{1}=-100x + 300$。
(2)解:货车从相遇点到$B$地还需时间:$120÷100 = 1.2h$,货车全程时间为$1.8 + 1.2 = 3h$,所以客车全程时间也为$3h$。
客车行驶路程为$180km$,速度为$180÷1.2 = 150km/h$,客车行驶时间为$3h$,则客车出发时间为$x = 3 - 3 = 0h$(此处根据题意应为货车先出发,设客车出发时间为$t$,则客车行驶时间为$3 - t$,相遇时货车行驶$1.8h$,客车行驶$1.8 - t$,路程$150(1.8 - t)=180$,解得$t = 0.6h$,即客车$x = 0.6h$出发,$x = 3h$到达,$y_{2}$过点$(0.6,0)$和$(3,180)$)。
图象与$x$轴交点表示客车出发的时间。
(注:由于无法直接画图,此处文字说明图象为过点$(0.6,0)$和$(3,180)$的线段)
货车速度为$100km/h$,行驶$1.8h$的路程为$100×1.8 = 180km$,此时距$B$地$120km$,则$A$、$B$两地距离为$180 + 120 = 300km$,即当$x = 0$时,$y_{1}=300$,所以$b = 300$。
又因为当$x = 1.8$时,$y_{1}=120$,代入得$1.8k + 300 = 120$,解得$k=-100$。
所以$y_{1}=-100x + 300$。
(2)解:货车从相遇点到$B$地还需时间:$120÷100 = 1.2h$,货车全程时间为$1.8 + 1.2 = 3h$,所以客车全程时间也为$3h$。
客车行驶路程为$180km$,速度为$180÷1.2 = 150km/h$,客车行驶时间为$3h$,则客车出发时间为$x = 3 - 3 = 0h$(此处根据题意应为货车先出发,设客车出发时间为$t$,则客车行驶时间为$3 - t$,相遇时货车行驶$1.8h$,客车行驶$1.8 - t$,路程$150(1.8 - t)=180$,解得$t = 0.6h$,即客车$x = 0.6h$出发,$x = 3h$到达,$y_{2}$过点$(0.6,0)$和$(3,180)$)。
图象与$x$轴交点表示客车出发的时间。
(注:由于无法直接画图,此处文字说明图象为过点$(0.6,0)$和$(3,180)$的线段)