1. 下列实数中,是无理数的是(
A.$\frac{22}{7}$
B.$\sqrt{3}$
C.$-3.14$
D.$\sqrt{4}$
B
).A.$\frac{22}{7}$
B.$\sqrt{3}$
C.$-3.14$
D.$\sqrt{4}$
答案:解:无理数是无限不循环小数。
A.$\frac{22}{7}$是分数,属于有理数;
B.$\sqrt{3}$是无限不循环小数,是无理数;
C.$-3.14$是有限小数,属于有理数;
D.$\sqrt{4}=2$,是整数,属于有理数。
故选B。
A.$\frac{22}{7}$是分数,属于有理数;
B.$\sqrt{3}$是无限不循环小数,是无理数;
C.$-3.14$是有限小数,属于有理数;
D.$\sqrt{4}=2$,是整数,属于有理数。
故选B。
2. 下列各组数作为三角形的三边长,其中能构成钝角三角形的是(
A.2,3,4
B.3,4,5
C.4,5,6
D.5,6,7
A
).A.2,3,4
B.3,4,5
C.4,5,6
D.5,6,7
答案:【解析】:
本题主要考察三角形的性质,特别是钝角三角形的判定。
对于选项A,$2^2 + 3^2 = 4 + 9 = 13$,而$4^2 = 16$,因为$13 \lt 16$,满足钝角三角形的条件(即最大边的平方大于其他两边的平方和),所以能构成钝角三角形。
对于选项B,$3^2 + 4^2 = 9 + 16 = 25$,且$5^2 = 25$,两边平方和等于最长边的平方,所以能构成直角三角形,不符合题意。
对于选项C,$4^2 + 5^2 = 16 + 25 = 41$,而$6^2 = 36$,因为$41 \gt 36$,所以能构成锐角三角形,不符合题意。
对于选项D,$5^2 + 6^2 = 25 + 36 = 61$,而$7^2 = 49$,因为$61 \gt 49$,所以能构成锐角三角形,不符合题意。
【答案】:
A
本题主要考察三角形的性质,特别是钝角三角形的判定。
对于选项A,$2^2 + 3^2 = 4 + 9 = 13$,而$4^2 = 16$,因为$13 \lt 16$,满足钝角三角形的条件(即最大边的平方大于其他两边的平方和),所以能构成钝角三角形。
对于选项B,$3^2 + 4^2 = 9 + 16 = 25$,且$5^2 = 25$,两边平方和等于最长边的平方,所以能构成直角三角形,不符合题意。
对于选项C,$4^2 + 5^2 = 16 + 25 = 41$,而$6^2 = 36$,因为$41 \gt 36$,所以能构成锐角三角形,不符合题意。
对于选项D,$5^2 + 6^2 = 25 + 36 = 61$,而$7^2 = 49$,因为$61 \gt 49$,所以能构成锐角三角形,不符合题意。
【答案】:
A
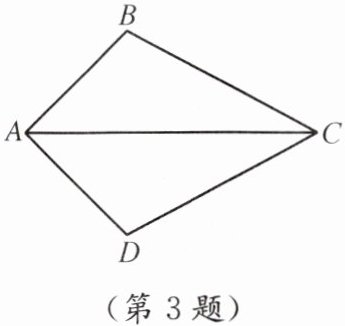
3. 如图,$\angle BAC= \angle DAC$,添加下列一个条件后,仍不能判定$\triangle ABC\cong\triangle ADC$的是(
A.$\angle B= \angle D$
B.$\angle BCA= \angle DCA$
C.$AB= AD$
D.$BC= DC$
D
).
A.$\angle B= \angle D$
B.$\angle BCA= \angle DCA$
C.$AB= AD$
D.$BC= DC$
答案:【解析】:本题可根据全等三角形的判定定理,逐一分析每个选项添加条件后是否能判定$\triangle ABC\cong\triangle ADC$。
全等三角形有以下$5$个判定定理:
$SSS$(边边边):三边对应相等的的三角形是全等三角形。
$SAS$(边角边):两边及其夹角对应相等的三角形是全等三角形。
$ASA$(角边角):两角及其夹边相等的三角形全等。
$AAS$(角角边):两角及其一角的对边相等的三角形全等。
$HL$(斜边、直角边):在一对直角三角形中,斜边及其另一条直角边相等的三角形全等。
选项A
已知$\angle BAC = \angle DAC$,当添加条件$\angle B = \angle D$时,在$\triangle ABC$和$\triangle ADC$中,$\angle BAC = \angle DAC$,$\angle B = \angle D$,$AC = AC$(公共边),此时满足全等三角形判定定理中的$AAS$,所以能判定$\triangle ABC\cong\triangle ADC$。
选项B
已知$\angle BAC = \angle DAC$,当添加条件$\angle BCA = \angle DCA$时,在$\triangle ABC$和$\triangle ADC$中,$\angle BAC = \angle DAC$,$\angle BCA = \angle DCA$,$AC = AC$(公共边),此时满足全等三角形判定定理中的$ASA$,所以能判定$\triangle ABC\cong\triangle ADC$。
选项C
已知$\angle BAC = \angle DAC$,当添加条件$AB = AD$时,在$\triangle ABC$和$\triangle ADC$中,$AB = AD$,$\angle BAC = \angle DAC$,$AC = AC$(公共边),此时满足全等三角形判定定理中的$SAS$,所以能判定$\triangle ABC\cong\triangle ADC$。
选项D
已知$\angle BAC = \angle DAC$,当添加条件$BC = DC$时,在$\triangle ABC$和$\triangle ADC$中,虽然有$\angle BAC = \angle DAC$,$BC = DC$,$AC = AC$(公共边),但是这是两边及其中一边的对角对应相等,不满足全等三角形的判定定理,所以不能判定$\triangle ABC\cong\triangle ADC$。
综上,答案选D。
【答案】:D
全等三角形有以下$5$个判定定理:
$SSS$(边边边):三边对应相等的的三角形是全等三角形。
$SAS$(边角边):两边及其夹角对应相等的三角形是全等三角形。
$ASA$(角边角):两角及其夹边相等的三角形全等。
$AAS$(角角边):两角及其一角的对边相等的三角形全等。
$HL$(斜边、直角边):在一对直角三角形中,斜边及其另一条直角边相等的三角形全等。
选项A
已知$\angle BAC = \angle DAC$,当添加条件$\angle B = \angle D$时,在$\triangle ABC$和$\triangle ADC$中,$\angle BAC = \angle DAC$,$\angle B = \angle D$,$AC = AC$(公共边),此时满足全等三角形判定定理中的$AAS$,所以能判定$\triangle ABC\cong\triangle ADC$。
选项B
已知$\angle BAC = \angle DAC$,当添加条件$\angle BCA = \angle DCA$时,在$\triangle ABC$和$\triangle ADC$中,$\angle BAC = \angle DAC$,$\angle BCA = \angle DCA$,$AC = AC$(公共边),此时满足全等三角形判定定理中的$ASA$,所以能判定$\triangle ABC\cong\triangle ADC$。
选项C
已知$\angle BAC = \angle DAC$,当添加条件$AB = AD$时,在$\triangle ABC$和$\triangle ADC$中,$AB = AD$,$\angle BAC = \angle DAC$,$AC = AC$(公共边),此时满足全等三角形判定定理中的$SAS$,所以能判定$\triangle ABC\cong\triangle ADC$。
选项D
已知$\angle BAC = \angle DAC$,当添加条件$BC = DC$时,在$\triangle ABC$和$\triangle ADC$中,虽然有$\angle BAC = \angle DAC$,$BC = DC$,$AC = AC$(公共边),但是这是两边及其中一边的对角对应相等,不满足全等三角形的判定定理,所以不能判定$\triangle ABC\cong\triangle ADC$。
综上,答案选D。
【答案】:D
4. 有下列结论:① 周长相等的两个等腰三角形全等;② 周长相等的两个正方形全等;③ 面积相等的两个等腰三角形全等;④ 面积相等的两个正方形全等. 其中,正确的是(
A.②③
B.①③
C.③④
D.②④
D
).A.②③
B.①③
C.③④
D.②④
答案:【解析】:
首先,我们逐一分析每个结论:
① 对于周长相等的两个等腰三角形,我们不能直接断定它们全等。因为等腰三角形只要求两边相等,但这两边以及底边的长度可以有很多种组合方式使得周长相等,但三角形形状并不相同。所以结论①是错误的。
② 对于周长相等的两个正方形,由于正方形的四条边都相等,如果两个正方形的周长相等,那么它们的每一条边都必然相等。根据SSS全等条件,这两个正方形必然全等。所以结论②是正确的。
③ 对于面积相等的两个等腰三角形,我们不能直接断定它们全等。因为等腰三角形的面积可以由底和高决定,即使面积相等,底和高的长度也可以有很多种组合方式,使得三角形的形状并不相同。所以结论③是错误的。
④ 对于面积相等的两个正方形,由于正方形的面积是边长的平方,如果两个正方形的面积相等,那么它们的边长必然相等。因此,这两个正方形必然全等。所以结论④是正确的。
综上所述,正确的结论是②和④。
【答案】:D
首先,我们逐一分析每个结论:
① 对于周长相等的两个等腰三角形,我们不能直接断定它们全等。因为等腰三角形只要求两边相等,但这两边以及底边的长度可以有很多种组合方式使得周长相等,但三角形形状并不相同。所以结论①是错误的。
② 对于周长相等的两个正方形,由于正方形的四条边都相等,如果两个正方形的周长相等,那么它们的每一条边都必然相等。根据SSS全等条件,这两个正方形必然全等。所以结论②是正确的。
③ 对于面积相等的两个等腰三角形,我们不能直接断定它们全等。因为等腰三角形的面积可以由底和高决定,即使面积相等,底和高的长度也可以有很多种组合方式,使得三角形的形状并不相同。所以结论③是错误的。
④ 对于面积相等的两个正方形,由于正方形的面积是边长的平方,如果两个正方形的面积相等,那么它们的边长必然相等。因此,这两个正方形必然全等。所以结论④是正确的。
综上所述,正确的结论是②和④。
【答案】:D
5. 一个正方形的面积是15,估计它的边长大小在(
A.5与6之间
B.4与5之间
C.3与4之间
D.2与3之间
C
).A.5与6之间
B.4与5之间
C.3与4之间
D.2与3之间
答案:解:设正方形的边长为$a$,则$a^2 = 15$,$a = \sqrt{15}$。
因为$9 < 15 < 16$,所以$\sqrt{9} < \sqrt{15} < \sqrt{16}$,即$3 < \sqrt{15} < 4$。
答案:C
因为$9 < 15 < 16$,所以$\sqrt{9} < \sqrt{15} < \sqrt{16}$,即$3 < \sqrt{15} < 4$。
答案:C
6. 如图,在四边形$ABCD$中,$\angle B= \angle D= 90^{\circ}$,分别以四边向外作正方形甲、乙、丙、丁,若用$S_{甲}$,$S_{乙}$,$S_{丙}$,$S_{丁}$分别表示它们的面积,下列结论正确的是(

A.$S_{甲}= S_{丁}$
B.$S_{乙}= S_{丙}$
C.$S_{甲}+S_{乙}= S_{丙}+S_{丁}$
D.$S_{甲}-S_{乙}= S_{丙}-S_{丁}$
C
).
A.$S_{甲}= S_{丁}$
B.$S_{乙}= S_{丙}$
C.$S_{甲}+S_{乙}= S_{丙}+S_{丁}$
D.$S_{甲}-S_{乙}= S_{丙}-S_{丁}$
答案:解:连接AC。
∵∠B=90°,
∴在Rt△ABC中,AB²+BC²=AC²。
∵∠D=90°,
∴在Rt△ADC中,AD²+CD²=AC²。
∴AB²+BC²=AD²+CD²。
∵S甲=AB²,S乙=BC²,S丙=CD²,S丁=AD²,
∴S甲+S乙=S丙+S丁。
C
∵∠B=90°,
∴在Rt△ABC中,AB²+BC²=AC²。
∵∠D=90°,
∴在Rt△ADC中,AD²+CD²=AC²。
∴AB²+BC²=AD²+CD²。
∵S甲=AB²,S乙=BC²,S丙=CD²,S丁=AD²,
∴S甲+S乙=S丙+S丁。
C