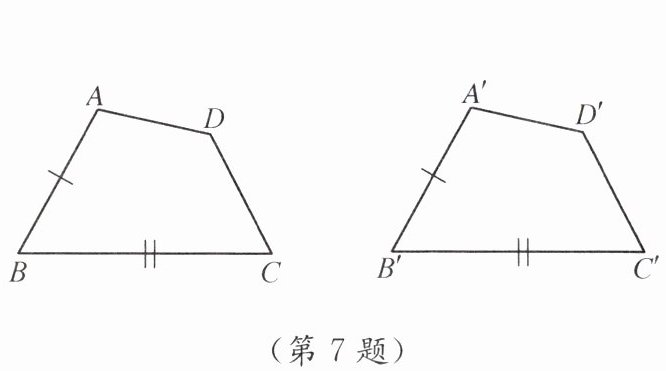
7. 如图,在四边形$ABCD与四边形A'B'C'D'$中,$AB= A'B'$,$\angle B= \angle B'$,$BC= B'C'$. 有下列条件:① $\angle A= \angle A'$,$AD= A'D'$;② $\angle A= \angle A'$,$CD= C'D'$;③ $\angle A= \angle A'$,$\angle D= \angle D'$;④ $AD= A'D'$,$CD= C'D'$. 添加其中一个,可使四边形$ABCD\cong四边形A'B'C'D'$. 上述条件中符合要求的有(
A.①②③
B.①③④
C.①④
D.①②③④
B
).
A.①②③
B.①③④
C.①④
D.①②③④
答案:解:连接AC、A'C'。
在△ABC和△A'B'C'中,
∵AB=A'B',∠B=∠B',BC=B'C',
∴△ABC≌△A'B'C'(SAS),
∴AC=A'C',∠BAC=∠B'A'C',∠BCA=∠B'C'A'。
①若∠A=∠A',AD=A'D',
∵∠BAD=∠B'A'D',∠BAC=∠B'A'C',
∴∠CAD=∠C'A'D',
在△ACD和△A'C'D'中,
AD=A'D',∠CAD=∠C'A'D',AC=A'C',
∴△ACD≌△A'C'D'(SAS),
∴CD=C'D',∠D=∠D',∠ACD=∠A'C'D',
∴∠BCD=∠B'C'D',
∴四边形ABCD≌四边形A'B'C'D'。
②若∠A=∠A',CD=C'D',无法证明△ACD≌△A'C'D',故不符合。
③若∠A=∠A',∠D=∠D',
∵∠BAD=∠B'A'D',∠BAC=∠B'A'C',
∴∠CAD=∠C'A'D',
在△ACD和△A'C'D'中,
∠CAD=∠C'A'D',∠D=∠D',AC=A'C',
∴△ACD≌△A'C'D'(AAS),
∴AD=A'D',CD=C'D',∠ACD=∠A'C'D',
∴∠BCD=∠B'C'D',
∴四边形ABCD≌四边形A'B'C'D'。
④若AD=A'D',CD=C'D',
在△ACD和△A'C'D'中,
AD=A'D',CD=C'D',AC=A'C',
∴△ACD≌△A'C'D'(SSS),
∴∠CAD=∠C'A'D',∠D=∠D',∠ACD=∠A'C'D',
∴∠BAD=∠B'A'D',∠BCD=∠B'C'D',
∴四边形ABCD≌四边形A'B'C'D'。
综上,①③④符合要求,答案选B。
在△ABC和△A'B'C'中,
∵AB=A'B',∠B=∠B',BC=B'C',
∴△ABC≌△A'B'C'(SAS),
∴AC=A'C',∠BAC=∠B'A'C',∠BCA=∠B'C'A'。
①若∠A=∠A',AD=A'D',
∵∠BAD=∠B'A'D',∠BAC=∠B'A'C',
∴∠CAD=∠C'A'D',
在△ACD和△A'C'D'中,
AD=A'D',∠CAD=∠C'A'D',AC=A'C',
∴△ACD≌△A'C'D'(SAS),
∴CD=C'D',∠D=∠D',∠ACD=∠A'C'D',
∴∠BCD=∠B'C'D',
∴四边形ABCD≌四边形A'B'C'D'。
②若∠A=∠A',CD=C'D',无法证明△ACD≌△A'C'D',故不符合。
③若∠A=∠A',∠D=∠D',
∵∠BAD=∠B'A'D',∠BAC=∠B'A'C',
∴∠CAD=∠C'A'D',
在△ACD和△A'C'D'中,
∠CAD=∠C'A'D',∠D=∠D',AC=A'C',
∴△ACD≌△A'C'D'(AAS),
∴AD=A'D',CD=C'D',∠ACD=∠A'C'D',
∴∠BCD=∠B'C'D',
∴四边形ABCD≌四边形A'B'C'D'。
④若AD=A'D',CD=C'D',
在△ACD和△A'C'D'中,
AD=A'D',CD=C'D',AC=A'C',
∴△ACD≌△A'C'D'(SSS),
∴∠CAD=∠C'A'D',∠D=∠D',∠ACD=∠A'C'D',
∴∠BAD=∠B'A'D',∠BCD=∠B'C'D',
∴四边形ABCD≌四边形A'B'C'D'。
综上,①③④符合要求,答案选B。
8. 如图,$\triangle ABC$中,点$E在边AC$上,$EB= EA$,$\angle A= 2\angle CBE$,$CD垂直于BE$的延长线,$D$为垂足. 若$BD= 8$,$AC= 11$,则$CD$的长是(

A.3.5
B.4
C.4.5
D.5
B
).
A.3.5
B.4
C.4.5
D.5
答案:解:设∠CBE = α,则∠A = 2α。
∵EB = EA,
∴∠EBA = ∠A = 2α,∠AEB = 180° - 4α。
∵∠AEB + ∠BEC = 180°,
∴∠BEC = 4α。
∵∠BEC = ∠EBC + ∠ECB,
∴∠ECB = 3α。
延长BD至F,使DF = CD,设CD = x,则DF = x,CF = √2x。
∵∠CDF = 90°,
∴∠CFD = 45°。
∵∠BCF = ∠ECB - ∠ECF = 3α - α = 2α = ∠A,∠BFC = ∠BEA = 180° - 4α,
∴△BFC∽△BEA,
∴BF/BE = BC/BA。
设EA = EB = m,则AC = EA + EC = m + EC = 11,
∴EC = 11 - m。
在△BEC中,由正弦定理:EB/sin∠ECB = EC/sin∠EBC,即m/sin3α = (11 - m)/sinα。
∵sin3α = 3sinα - 4sin³α,
∴m/(3 - 4sin²α) = 11 - m,解得sin²α = (3m - 11 + m)/(4m) = (4m - 11)/(4m)。
在Rt△BCD中,BC = √(BD² + CD²) = √(64 + x²)。
在△ABC中,∠A = 2α,∠ABC = 3α,∠ACB = 3α,
∴AB = BC = √(64 + x²)。
BF = BD + DF = 8 + x,BE = m,由△BFC∽△BEA得(8 + x)/m = √(64 + x²)/√(64 + x²) = 1,
∴8 + x = m。
∵BF = BE,
∴8 + x = m。
又
∵EC = 11 - m = 11 - (8 + x) = 3 - x。
在Rt△CDE中,∠CED = ∠BEC = 4α,∠CDE = 90°,
∴∠ECD = 90° - 4α = α,
∴EC = CD/cosα,即3 - x = x/cosα,
∴cosα = x/(3 - x)。
∵sin²α + cos²α = 1,
∴(4m - 11)/(4m) + (x²)/(3 - x)² = 1。
将m = 8 + x代入得(4(8 + x) - 11)/(4(8 + x)) + x²/(3 - x)² = 1,化简得(21 + 4x)/(4(8 + x)) + x²/(3 - x)² = 1。
解得x = 3(舍去)或x = 4。
∴CD = 4。
答案:B
∵EB = EA,
∴∠EBA = ∠A = 2α,∠AEB = 180° - 4α。
∵∠AEB + ∠BEC = 180°,
∴∠BEC = 4α。
∵∠BEC = ∠EBC + ∠ECB,
∴∠ECB = 3α。
延长BD至F,使DF = CD,设CD = x,则DF = x,CF = √2x。
∵∠CDF = 90°,
∴∠CFD = 45°。
∵∠BCF = ∠ECB - ∠ECF = 3α - α = 2α = ∠A,∠BFC = ∠BEA = 180° - 4α,
∴△BFC∽△BEA,
∴BF/BE = BC/BA。
设EA = EB = m,则AC = EA + EC = m + EC = 11,
∴EC = 11 - m。
在△BEC中,由正弦定理:EB/sin∠ECB = EC/sin∠EBC,即m/sin3α = (11 - m)/sinα。
∵sin3α = 3sinα - 4sin³α,
∴m/(3 - 4sin²α) = 11 - m,解得sin²α = (3m - 11 + m)/(4m) = (4m - 11)/(4m)。
在Rt△BCD中,BC = √(BD² + CD²) = √(64 + x²)。
在△ABC中,∠A = 2α,∠ABC = 3α,∠ACB = 3α,
∴AB = BC = √(64 + x²)。
BF = BD + DF = 8 + x,BE = m,由△BFC∽△BEA得(8 + x)/m = √(64 + x²)/√(64 + x²) = 1,
∴8 + x = m。
∵BF = BE,
∴8 + x = m。
又
∵EC = 11 - m = 11 - (8 + x) = 3 - x。
在Rt△CDE中,∠CED = ∠BEC = 4α,∠CDE = 90°,
∴∠ECD = 90° - 4α = α,
∴EC = CD/cosα,即3 - x = x/cosα,
∴cosα = x/(3 - x)。
∵sin²α + cos²α = 1,
∴(4m - 11)/(4m) + (x²)/(3 - x)² = 1。
将m = 8 + x代入得(4(8 + x) - 11)/(4(8 + x)) + x²/(3 - x)² = 1,化简得(21 + 4x)/(4(8 + x)) + x²/(3 - x)² = 1。
解得x = 3(舍去)或x = 4。
∴CD = 4。
答案:B
9. 4的平方根是
$\pm 2$
,8的立方根是$2$
.答案:【解析】:
本题主要考察平方根和立方根的定义及计算。
对于4的平方根,我们需要找到一个数,使得这个数的平方等于4。
根据平方根的定义,一个正数的平方根有两个,它们互为相反数。
因此,4的平方根是$\pm 2$。
对于8的立方根,我们需要找到一个数,使得这个数的立方等于8。
根据立方根的定义,一个数的立方根只有一个。
因此,8的立方根是2。
【答案】:
$\pm 2$;$2$
本题主要考察平方根和立方根的定义及计算。
对于4的平方根,我们需要找到一个数,使得这个数的平方等于4。
根据平方根的定义,一个正数的平方根有两个,它们互为相反数。
因此,4的平方根是$\pm 2$。
对于8的立方根,我们需要找到一个数,使得这个数的立方等于8。
根据立方根的定义,一个数的立方根只有一个。
因此,8的立方根是2。
【答案】:
$\pm 2$;$2$
10. 比较大小:$-\sqrt{3}$
>
$-2$.(填“>”“<”或“=”)答案:解:因为$\sqrt{3}\approx1.732$,所以$\vert -\sqrt{3}\vert=\sqrt{3}\approx1.732$,$\vert -2\vert=2$。
由于$1.732\lt2$,根据两个负数比较大小,绝对值大的反而小,可得$-\sqrt{3}\gt -2$。
$\gt$
由于$1.732\lt2$,根据两个负数比较大小,绝对值大的反而小,可得$-\sqrt{3}\gt -2$。
$\gt$
11. 如图,已知两个三角形全等,根据图中提供的信息,可得$EF$的长为
20
.答案:【解析】:
本题可根据全等三角形的性质来求解$EF$的长,全等三角形的对应边相等,我们需要先找出与$\triangle ABC$全等的$\triangle DEF$中对应的边,再根据已知条件计算出$EF$的长度。
已知两个三角形全等,观察图形可知$\triangle ABC$与$\triangle DEF$全等,其中$\angle A=\angle D = 60^{\circ}$,$\angle B=\angle E = 50^{\circ}$,$\angle C=\angle F = 70^{\circ}$,$AC$与$DF$是对应边,$AB$与$DE$是对应边,$BC$与$EF$是对应边。
因为$BC = 20$,根据全等三角形对应边相等的性质,可得$EF=BC = 20$。
【答案】:
$20$
本题可根据全等三角形的性质来求解$EF$的长,全等三角形的对应边相等,我们需要先找出与$\triangle ABC$全等的$\triangle DEF$中对应的边,再根据已知条件计算出$EF$的长度。
已知两个三角形全等,观察图形可知$\triangle ABC$与$\triangle DEF$全等,其中$\angle A=\angle D = 60^{\circ}$,$\angle B=\angle E = 50^{\circ}$,$\angle C=\angle F = 70^{\circ}$,$AC$与$DF$是对应边,$AB$与$DE$是对应边,$BC$与$EF$是对应边。
因为$BC = 20$,根据全等三角形对应边相等的性质,可得$EF=BC = 20$。
【答案】:
$20$
12. 如图,在长方形$OABC$中,$OC= 2$,$OA= 1$. 以原点$O$为圆心,对角线$OB的长为半径画弧交数轴于点D$,则数轴上点$D$表示的数是
$-\sqrt{5}$
.答案:【解析】:
本题可先根据长方形的性质和勾股定理求出$OB$的长度,再结合点$D$的位置确定点$D$表示的数。
步骤一:求$OB$的长度
在长方形$OABC$中,$\angle OCB = 90^{\circ}$,已知$OC = 2$,$OA = 1$,因为$OA$与$BC$是长方形的对边,所以$BC = OA = 1$。
在$Rt\triangle OBC$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得$OB=\sqrt{OC^{2}+BC^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{4 + 1}=\sqrt{5}$。
步骤二:确定点$D$表示的数
因为以原点$O$为圆心,$OB$的长为半径画弧交数轴于点$D$,所以$OD = OB = \sqrt{5}$。
又因为点$D$在原点$O$的左侧,在数轴上原点左侧的数为负数,所以点$D$表示的数是$-\sqrt{5}$。
【答案】:$-\sqrt{5}$
本题可先根据长方形的性质和勾股定理求出$OB$的长度,再结合点$D$的位置确定点$D$表示的数。
步骤一:求$OB$的长度
在长方形$OABC$中,$\angle OCB = 90^{\circ}$,已知$OC = 2$,$OA = 1$,因为$OA$与$BC$是长方形的对边,所以$BC = OA = 1$。
在$Rt\triangle OBC$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得$OB=\sqrt{OC^{2}+BC^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{4 + 1}=\sqrt{5}$。
步骤二:确定点$D$表示的数
因为以原点$O$为圆心,$OB$的长为半径画弧交数轴于点$D$,所以$OD = OB = \sqrt{5}$。
又因为点$D$在原点$O$的左侧,在数轴上原点左侧的数为负数,所以点$D$表示的数是$-\sqrt{5}$。
【答案】:$-\sqrt{5}$
13. 如图,在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,$AC= BC$,$AD是\angle CAB$的平分线,过点$B作BE\perp AD$,交$AD的延长线于点E$. 若$AD= 3$,则$BE$的长为______
$\frac{3}{2}$
.答案:解:延长AC、BE交于点F。
∵AD平分∠CAB,BE⊥AE,
∴∠FAE=∠BAE,∠AEF=∠AEB=90°。
在△AEF和△AEB中,
∠FAE=∠BAE,AE=AE,∠AEF=∠AEB,
∴△AEF≌△AEB(ASA),∴BE=EF=1/2BF。
∵∠C=90°,BE⊥AE,
∴∠CAD+∠ADC=90°,∠EBD+∠BDE=90°。
∵∠ADC=∠BDE,∴∠CAD=∠EBD。
在△ACD和△BCF中,
∠CAD=∠CBF,AC=BC,∠ACD=∠BCF=90°,
∴△ACD≌△BCF(ASA),∴AD=BF=3。
∵BE=1/2BF,∴BE=3/2。
答案:3/2
∵AD平分∠CAB,BE⊥AE,
∴∠FAE=∠BAE,∠AEF=∠AEB=90°。
在△AEF和△AEB中,
∠FAE=∠BAE,AE=AE,∠AEF=∠AEB,
∴△AEF≌△AEB(ASA),∴BE=EF=1/2BF。
∵∠C=90°,BE⊥AE,
∴∠CAD+∠ADC=90°,∠EBD+∠BDE=90°。
∵∠ADC=∠BDE,∴∠CAD=∠EBD。
在△ACD和△BCF中,
∠CAD=∠CBF,AC=BC,∠ACD=∠BCF=90°,
∴△ACD≌△BCF(ASA),∴AD=BF=3。
∵BE=1/2BF,∴BE=3/2。
答案:3/2
14. 如图,$AD为\triangle ABC$的角平分线,$\angle C= 90^{\circ}$,$AC= 3$,$AB= 5$,则$AD$的长度为______.


$\frac{3\sqrt{5}}{2}$
答案:解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理得BC=$\sqrt{AB^2 - AC^2}=\sqrt{5^2 - 3^2}=4$。
设CD=x,则BD=BC - CD=4 - x。
∵AD为△ABC的角平分线,
∴$\frac{AB}{AC}=\frac{BD}{CD}$,即$\frac{5}{3}=\frac{4 - x}{x}$,
解得x=$\frac{3}{2}$。
在Rt△ACD中,AD=$\sqrt{AC^2 + CD^2}=\sqrt{3^2 + (\frac{3}{2})^2}=\frac{3\sqrt{5}}{2}$。
$\frac{3\sqrt{5}}{2}$
由勾股定理得BC=$\sqrt{AB^2 - AC^2}=\sqrt{5^2 - 3^2}=4$。
设CD=x,则BD=BC - CD=4 - x。
∵AD为△ABC的角平分线,
∴$\frac{AB}{AC}=\frac{BD}{CD}$,即$\frac{5}{3}=\frac{4 - x}{x}$,
解得x=$\frac{3}{2}$。
在Rt△ACD中,AD=$\sqrt{AC^2 + CD^2}=\sqrt{3^2 + (\frac{3}{2})^2}=\frac{3\sqrt{5}}{2}$。
$\frac{3\sqrt{5}}{2}$