15. 计算:$\sqrt[3]{8}-(\sqrt{3})^{2}+\sqrt{25}$.
答案:【解析】:
本题主要考察立方根、平方根以及算术平方根的计算。
首先,我们分别计算每个部分:
1. 计算立方根 $\sqrt[3]{8}$:
$\sqrt[3]{8} = 2$
2. 计算平方 $(\sqrt{3})^{2}$:
$(\sqrt{3})^{2} = 3$
3. 计算算术平方根 $\sqrt{25}$:
$\sqrt{25} = 5$
然后,将上述结果代入原式进行计算:
$\sqrt[3]{8} - (\sqrt{3})^{2} + \sqrt{25} = 2 - 3 + 5$
【答案】:
解:原式= $\sqrt[3]{8} - (\sqrt{3})^{2} + \sqrt{25}$
= $2 - 3 + 5$
= $4$。
本题主要考察立方根、平方根以及算术平方根的计算。
首先,我们分别计算每个部分:
1. 计算立方根 $\sqrt[3]{8}$:
$\sqrt[3]{8} = 2$
2. 计算平方 $(\sqrt{3})^{2}$:
$(\sqrt{3})^{2} = 3$
3. 计算算术平方根 $\sqrt{25}$:
$\sqrt{25} = 5$
然后,将上述结果代入原式进行计算:
$\sqrt[3]{8} - (\sqrt{3})^{2} + \sqrt{25} = 2 - 3 + 5$
【答案】:
解:原式= $\sqrt[3]{8} - (\sqrt{3})^{2} + \sqrt{25}$
= $2 - 3 + 5$
= $4$。
16. 解方程:
(1)$8x^{2}= 50$;
(2)$(x-2)^{3}+27= 0$.
(1)$8x^{2}= 50$;
(2)$(x-2)^{3}+27= 0$.
答案:(1)解:$8x^{2}=50$
$x^{2}=\frac{50}{8}=\frac{25}{4}$
$x=\pm\sqrt{\frac{25}{4}}$
$x=\pm\frac{5}{2}$
(2)解:$(x - 2)^{3}+27=0$
$(x - 2)^{3}=-27$
$x - 2=\sqrt[3]{-27}$
$x - 2=-3$
$x=-1$
$x^{2}=\frac{50}{8}=\frac{25}{4}$
$x=\pm\sqrt{\frac{25}{4}}$
$x=\pm\frac{5}{2}$
(2)解:$(x - 2)^{3}+27=0$
$(x - 2)^{3}=-27$
$x - 2=\sqrt[3]{-27}$
$x - 2=-3$
$x=-1$
17. 如图,点$C$,$E在边BF$上,$BE= CF$,$AB// DE$,$\angle A= \angle D$. 求证:$AC= DF$.
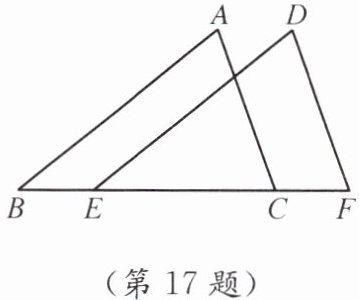

答案:【解析】:本题考查全等三角形的证明,根据题目已知条件,$BE=CF$,$AB // DE$,$\angle A = \angle D$,可以利用这些条件通过全等三角形的判定定理来证明$AC = DF$。
由于$AB // DE$,根据两直线平行,同位角相等,可得$\angle B = \angle DEF$。
又因为$BE = CF$,那么$BE + EC = CF + EC$,即$BC = EF$。
在$\triangle ABC$和$\triangle DEF$中:
$\angle A = \angle D$(已知)
$\angle B = \angle DEF$(已证)
$BC = EF$(已证)
根据全等三角形判定定理中的$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可以得出$\triangle ABC\cong\triangle DEF$。
根据全等三角形的性质,全等三角形的对应边相等,所以$AC = DF$。
【答案】:
证明:
∵$AB // DE$,
∴$\angle B = \angle DEF$。
∵$BE = CF$,
∴$BE + EC = CF + EC$,即$BC = EF$。
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases}\angle A = \angle D \\ \angle B = \angle DEF \\ BC = EF\end{cases}$
∴$\triangle ABC\cong\triangle DEF(AAS)$。
∴$AC = DF$。
由于$AB // DE$,根据两直线平行,同位角相等,可得$\angle B = \angle DEF$。
又因为$BE = CF$,那么$BE + EC = CF + EC$,即$BC = EF$。
在$\triangle ABC$和$\triangle DEF$中:
$\angle A = \angle D$(已知)
$\angle B = \angle DEF$(已证)
$BC = EF$(已证)
根据全等三角形判定定理中的$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可以得出$\triangle ABC\cong\triangle DEF$。
根据全等三角形的性质,全等三角形的对应边相等,所以$AC = DF$。
【答案】:
证明:
∵$AB // DE$,
∴$\angle B = \angle DEF$。
∵$BE = CF$,
∴$BE + EC = CF + EC$,即$BC = EF$。
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases}\angle A = \angle D \\ \angle B = \angle DEF \\ BC = EF\end{cases}$
∴$\triangle ABC\cong\triangle DEF(AAS)$。
∴$AC = DF$。
18. 如图,$AD为\triangle ABC$的高,$AB= 17$,$BC= 9$,$AC= 10$,求$AD$的长.


答案:【解析】:本题可根据勾股定理分别表示出$BD$、$CD$的长度,再结合$BC$的长度列出方程,进而求出$AD$的长。
设$BD = x$,因为$BC = 9$,所以$CD=9 - x$。
在$Rt\triangle ABD$中,根据勾股定理$AB^{2}=BD^{2}+AD^{2}$,已知$AB = 17$,则$AD^{2}=AB^{2}-BD^{2}=17^{2}-x^{2}$。
在$Rt\triangle ACD$中,根据勾股定理$AC^{2}=CD^{2}+AD^{2}$,已知$AC = 10$,则$AD^{2}=AC^{2}-CD^{2}=10^{2}-(9 - x)^{2}$。
由于$AD^{2}$的值是固定的,所以可得方程$17^{2}-x^{2}=10^{2}-(9 - x)^{2}$,解方程求出$x$的值,再代入$AD^{2}=17^{2}-x^{2}$求出$AD$的长。
【答案】:解:设$BD = x$,则$CD = 9 - x$。
在$Rt\triangle ABD$中,$AD^{2}=AB^{2}-BD^{2}=17^{2}-x^{2}$。
在$Rt\triangle ACD$中,$AD^{2}=AC^{2}-CD^{2}=10^{2}-(9 - x)^{2}$。
所以$17^{2}-x^{2}=10^{2}-(9 - x)^{2}$,
即$289 - x^{2}=100-(81 - 18x + x^{2})$,
$289 - x^{2}=100 - 81 + 18x - x^{2}$,
$-x^{2}+x^{2}-18x=100 - 81 - 289$,
$-18x=-270$,
解得$x = 15$。
则$AD^{2}=17^{2}-15^{2}=(17 + 15)×(17 - 15)=32×2 = 64$,
所以$AD = 8$。
综上,$AD$的长为$8$。
设$BD = x$,因为$BC = 9$,所以$CD=9 - x$。
在$Rt\triangle ABD$中,根据勾股定理$AB^{2}=BD^{2}+AD^{2}$,已知$AB = 17$,则$AD^{2}=AB^{2}-BD^{2}=17^{2}-x^{2}$。
在$Rt\triangle ACD$中,根据勾股定理$AC^{2}=CD^{2}+AD^{2}$,已知$AC = 10$,则$AD^{2}=AC^{2}-CD^{2}=10^{2}-(9 - x)^{2}$。
由于$AD^{2}$的值是固定的,所以可得方程$17^{2}-x^{2}=10^{2}-(9 - x)^{2}$,解方程求出$x$的值,再代入$AD^{2}=17^{2}-x^{2}$求出$AD$的长。
【答案】:解:设$BD = x$,则$CD = 9 - x$。
在$Rt\triangle ABD$中,$AD^{2}=AB^{2}-BD^{2}=17^{2}-x^{2}$。
在$Rt\triangle ACD$中,$AD^{2}=AC^{2}-CD^{2}=10^{2}-(9 - x)^{2}$。
所以$17^{2}-x^{2}=10^{2}-(9 - x)^{2}$,
即$289 - x^{2}=100-(81 - 18x + x^{2})$,
$289 - x^{2}=100 - 81 + 18x - x^{2}$,
$-x^{2}+x^{2}-18x=100 - 81 - 289$,
$-18x=-270$,
解得$x = 15$。
则$AD^{2}=17^{2}-15^{2}=(17 + 15)×(17 - 15)=32×2 = 64$,
所以$AD = 8$。
综上,$AD$的长为$8$。