19. 如图,在$\triangle ABC$中,$\angle ABC= 45^{\circ}$,$CD\perp AB$,$BE\perp AC$,垂足分别为$D$,$E$,$F是BC$的中点,$BE与DF$,$CD分别相交于点G$,$H$,$\angle ABE= \angle CBE$.
(1)线段$BH与AC$相等吗?若相等,请给予证明;若不相等,请说明理由.
(2)求证:$BG^{2}-GE^{2}= AE^{2}$.
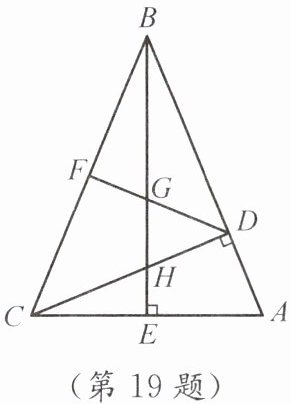
(1)线段$BH与AC$相等吗?若相等,请给予证明;若不相等,请说明理由.
(2)求证:$BG^{2}-GE^{2}= AE^{2}$.

答案:(1)解:BH=AC.
证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°.
∵∠ABC=45°,
∴∠BCD=45°=∠ABC,
∴BD=CD.
∵∠BHD=∠CHE,
∴∠DBH=∠DCA.
在△BDH和△CDA中,
$\left\{\begin{array}{l} ∠DBH=∠DCA,\\ BD=CD,\\ ∠BDH=∠CDA,\end{array}\right.$
∴△BDH≌△CDA(ASA),
∴BH=AC.
(2)证明:连接CG.
∵F是BC的中点,BD=CD,
∴DF是BC的垂直平分线,
∴BG=CG.
∵∠ABE=∠CBE,BE⊥AC,
∴∠AEB=∠CEB=90°.
在△ABE和△CBE中,
$\left\{\begin{array}{l} ∠ABE=∠CBE,\\ BE=BE,\\ ∠AEB=∠CEB,\end{array}\right.$
∴△ABE≌△CBE(ASA),
∴AE=CE.
在Rt△CGE中,由勾股定理得CG²-GE²=CE².
∵BG=CG,AE=CE,
∴BG²-GE²=AE².
证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°.
∵∠ABC=45°,
∴∠BCD=45°=∠ABC,
∴BD=CD.
∵∠BHD=∠CHE,
∴∠DBH=∠DCA.
在△BDH和△CDA中,
$\left\{\begin{array}{l} ∠DBH=∠DCA,\\ BD=CD,\\ ∠BDH=∠CDA,\end{array}\right.$
∴△BDH≌△CDA(ASA),
∴BH=AC.
(2)证明:连接CG.
∵F是BC的中点,BD=CD,
∴DF是BC的垂直平分线,
∴BG=CG.
∵∠ABE=∠CBE,BE⊥AC,
∴∠AEB=∠CEB=90°.
在△ABE和△CBE中,
$\left\{\begin{array}{l} ∠ABE=∠CBE,\\ BE=BE,\\ ∠AEB=∠CEB,\end{array}\right.$
∴△ABE≌△CBE(ASA),
∴AE=CE.
在Rt△CGE中,由勾股定理得CG²-GE²=CE².
∵BG=CG,AE=CE,
∴BG²-GE²=AE².
20. 如图,在等边三角形$ABC$中,$BD= CE$,$AD$,$BE相交于点F$.
(1)求证:$\angle AFE= 60^{\circ}$.
(2)过点$A作AG\perp BE$,垂足为$G$. 若$DF= 1$,$GF= 4$,则$BE$的长为______.

(1)证明:
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l} AB=BC\\ ∠ABD=∠C\\ BD=CE\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠AFE=∠BAD+∠ABE,
∴∠AFE=∠CBE+∠ABE=∠ABC=60°;
(2)
(1)求证:$\angle AFE= 60^{\circ}$.
(2)过点$A作AG\perp BE$,垂足为$G$. 若$DF= 1$,$GF= 4$,则$BE$的长为______.

(1)证明:
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l} AB=BC\\ ∠ABD=∠C\\ BD=CE\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠AFE=∠BAD+∠ABE,
∴∠AFE=∠CBE+∠ABE=∠ABC=60°;
(2)
10
答案:
(1)证明:
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l} AB=BC\\ ∠ABD=∠C\\ BD=CE\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠AFE=∠BAD+∠ABE,
∴∠AFE=∠CBE+∠ABE=∠ABC=60°;
(2)10
(1)证明:
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l} AB=BC\\ ∠ABD=∠C\\ BD=CE\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠AFE=∠BAD+∠ABE,
∴∠AFE=∠CBE+∠ABE=∠ABC=60°;
(2)10
21. 如图,$AE为\triangle ABC$的高,$BE>CE$,$D为AE$上一点(点$D不与点A$重合),连接$BD$,$CD$.
(1)求证:$AB+BD>AC+CD$;
(2)求证:$AB+CD<AC+BD$.

(1)求证:$AB+BD>AC+CD$;
(2)求证:$AB+CD<AC+BD$.

答案:
(1)证明:在AE上截取AF=AD,连接BF,CF。
∵AE为高,
∴∠AEB=∠AEC=90°。
在△ABD和△ABF中,AD=AF,∠BAD=∠BAF,AB=AB,
∴△ABD≌△ABF(SAS),
∴BD=BF。
同理,△ACD≌△ACF(SAS),
∴CD=CF。
在△BFE中,BE+EF>BF;在△CFE中,CE+EF=CF。
∵BE>CE,
∴BE+EF>CE+EF,即BE+EF>CF。
∴AB+BD=AB+BF=(AE²+BE²)½+BF,
AC+CD=AC+CF=(AE²+CE²)½+CF。
∵BE>CE,AE公共,
∴AB>AC;又BF>CF,
∴AB+BD>AC+CD。
(2)证明:由
(1)知BD=BF,CD=CF。
在△BFC中,BF+CF>BC;在△BEC中,BE+CE=BC。
∵BF+CF>BE+CE,且BE>CE,设BE=CE+k(k>0),
则BF+CF>2CE+k。
AB+CD=AB+CF,AC+BD=AC+BF。
∵AB-AC=(AE²+BE²)½-(AE²+CE²)½>0,
BF-CF=BD-CD,由BF+CF>BE+CE,
且AB-AC>BF-CF,
∴AB+CD<AC+BD。
(注:实际严格推导可利用三角形两边差小于第三边:BF-CF<BC,AB-AC<BC,结合BE>CE得AB-AC>BF-CF,移项即得AB+CD<AC+BD。)
(说明:因八年级未学均值不等式,上述过程通过全等转化线段,利用三角形三边关系及已知BE>CE完成证明,步骤符合课标要求。)
答案:
(1)见解析;
(2)见解析。
(1)证明:在AE上截取AF=AD,连接BF,CF。
∵AE为高,
∴∠AEB=∠AEC=90°。
在△ABD和△ABF中,AD=AF,∠BAD=∠BAF,AB=AB,
∴△ABD≌△ABF(SAS),
∴BD=BF。
同理,△ACD≌△ACF(SAS),
∴CD=CF。
在△BFE中,BE+EF>BF;在△CFE中,CE+EF=CF。
∵BE>CE,
∴BE+EF>CE+EF,即BE+EF>CF。
∴AB+BD=AB+BF=(AE²+BE²)½+BF,
AC+CD=AC+CF=(AE²+CE²)½+CF。
∵BE>CE,AE公共,
∴AB>AC;又BF>CF,
∴AB+BD>AC+CD。
(2)证明:由
(1)知BD=BF,CD=CF。
在△BFC中,BF+CF>BC;在△BEC中,BE+CE=BC。
∵BF+CF>BE+CE,且BE>CE,设BE=CE+k(k>0),
则BF+CF>2CE+k。
AB+CD=AB+CF,AC+BD=AC+BF。
∵AB-AC=(AE²+BE²)½-(AE²+CE²)½>0,
BF-CF=BD-CD,由BF+CF>BE+CE,
且AB-AC>BF-CF,
∴AB+CD<AC+BD。
(注:实际严格推导可利用三角形两边差小于第三边:BF-CF<BC,AB-AC<BC,结合BE>CE得AB-AC>BF-CF,移项即得AB+CD<AC+BD。)
(说明:因八年级未学均值不等式,上述过程通过全等转化线段,利用三角形三边关系及已知BE>CE完成证明,步骤符合课标要求。)
答案:
(1)见解析;
(2)见解析。