22. 给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形.
(1)用你学过的特殊四边形知识,写出两种勾股四边形的名称.
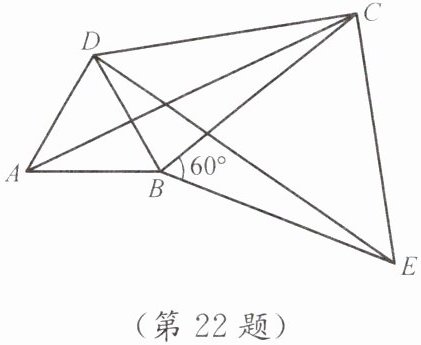
(2)如图,将$\triangle ABC绕顶点B按顺时针方向旋转60^{\circ}后得到\triangle DBE$,连接$AD$,$DC$,$CE$,已知$\angle DCB= 30^{\circ}$.
① 求证:$\triangle BCE$是等边三角形.
② 求证:$DC^{2}+BC^{2}= AC^{2}$(即四边形$ABCD$是勾股四边形).
(1)用你学过的特殊四边形知识,写出两种勾股四边形的名称.
(2)如图,将$\triangle ABC绕顶点B按顺时针方向旋转60^{\circ}后得到\triangle DBE$,连接$AD$,$DC$,$CE$,已知$\angle DCB= 30^{\circ}$.
① 求证:$\triangle BCE$是等边三角形.
② 求证:$DC^{2}+BC^{2}= AC^{2}$(即四边形$ABCD$是勾股四边形).

答案:(1)矩形、正方形
(2)①证明:∵△ABC绕顶点B顺时针旋转60°得到△DBE,
∴BC=BE,∠CBE=60°,
∴△BCE是等边三角形.
②证明:由①知△BCE是等边三角形,
∴CE=BC,∠BCE=60°.
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=30°+60°=90°.
在Rt△DCE中,DC²+CE²=DE².
∵△ABC绕顶点B旋转得到△DBE,
∴DE=AC,
又∵CE=BC,
∴DC²+BC²=AC².
(2)①证明:∵△ABC绕顶点B顺时针旋转60°得到△DBE,
∴BC=BE,∠CBE=60°,
∴△BCE是等边三角形.
②证明:由①知△BCE是等边三角形,
∴CE=BC,∠BCE=60°.
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=30°+60°=90°.
在Rt△DCE中,DC²+CE²=DE².
∵△ABC绕顶点B旋转得到△DBE,
∴DE=AC,
又∵CE=BC,
∴DC²+BC²=AC².
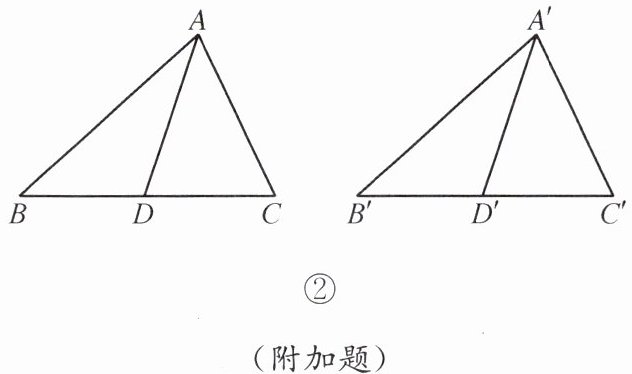
(1)如图①,$AD和A'D'分别是\triangle ABC和\triangle A'B'C'的边BC和边B'C'$上的中线,$AD= A'D'$,$AB= A'B'$,$BC= B'C'$. 求证:$\triangle ABC\cong\triangle A'B'C'$.

(2)如图②,$AD和A'D'分别是\triangle ABC和\triangle A'B'C'的边BC和边B'C'$上的中线,$AD= A'D'$,$AB= A'B'$,$AC= A'C'$. 判断$\triangle ABC与\triangle A'B'C'$是否仍然全等,并说明理由.
(3)类比上述问题的探究过程,下列命题是真命题的是______.(填写相应的序号)
① 两角和第三个角的平分线分别相等的两个三角形全等;
② 一边和这条边上的中线以及高分别相等的两个三角形全等;
③ 斜边和斜边上的高分别相等的两个直角三角形全等;
④ 两边和第三条边上的高分别相等的两个三角形全等;
⑤ 底边和一腰上的中线分别相等的两个等腰三角形全等.

证明:∵AD和A'D'分别是△ABC和△A'B'C'的中线,BC=B'C',
∴BD=B'D',DC=D'C'。
在△ABD和△A'B'D'中,
AB=A'B',AD=A'D',BD=B'D',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'。
在△ABC和△A'B'C'中,
AB=A'B',∠B=∠B',BC=B'C',
∴△ABC≌△A'B'C'(SAS)。
∴BD=B'D',DC=D'C'。
在△ABD和△A'B'D'中,
AB=A'B',AD=A'D',BD=B'D',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'。
在△ABC和△A'B'C'中,
AB=A'B',∠B=∠B',BC=B'C',
∴△ABC≌△A'B'C'(SAS)。
(2)如图②,$AD和A'D'分别是\triangle ABC和\triangle A'B'C'的边BC和边B'C'$上的中线,$AD= A'D'$,$AB= A'B'$,$AC= A'C'$. 判断$\triangle ABC与\triangle A'B'C'$是否仍然全等,并说明理由.

△ABC≌△A'B'C'。理由如下:
延长AD至点E,使DE=AD,连接BE;延长A'D'至点E',使D'E'=A'D',连接B'E'。
∵AD是△ABC的中线,
∴BD=DC。
在△ADC和△EDB中,
AD=ED,∠ADC=∠EDB,DC=BD,
∴△ADC≌△EDB(SAS),
∴AC=EB。
同理可得A'C'=E'B'。
∵AC=A'C',
∴EB=E'B'。
∵AD=A'D',
∴AE=A'E'。
在△ABE和△A'B'E'中,
AB=A'B',BE=B'E',AE=A'E',
∴△ABE≌△A'B'E'(SSS),
∴∠BAE=∠B'A'E',∠E=∠E'。
∵∠E=∠CAD,∠E'=∠C'A'D',
∴∠CAD=∠C'A'D',
∴∠BAC=∠B'A'C'。
在△ABC和△A'B'C'中,
AB=A'B',∠BAC=∠B'A'C',AC=A'C',
∴△ABC≌△A'B'C'(SAS)。
延长AD至点E,使DE=AD,连接BE;延长A'D'至点E',使D'E'=A'D',连接B'E'。
∵AD是△ABC的中线,
∴BD=DC。
在△ADC和△EDB中,
AD=ED,∠ADC=∠EDB,DC=BD,
∴△ADC≌△EDB(SAS),
∴AC=EB。
同理可得A'C'=E'B'。
∵AC=A'C',
∴EB=E'B'。
∵AD=A'D',
∴AE=A'E'。
在△ABE和△A'B'E'中,
AB=A'B',BE=B'E',AE=A'E',
∴△ABE≌△A'B'E'(SSS),
∴∠BAE=∠B'A'E',∠E=∠E'。
∵∠E=∠CAD,∠E'=∠C'A'D',
∴∠CAD=∠C'A'D',
∴∠BAC=∠B'A'C'。
在△ABC和△A'B'C'中,
AB=A'B',∠BAC=∠B'A'C',AC=A'C',
∴△ABC≌△A'B'C'(SAS)。
(3)类比上述问题的探究过程,下列命题是真命题的是______.(填写相应的序号)
① 两角和第三个角的平分线分别相等的两个三角形全等;
② 一边和这条边上的中线以及高分别相等的两个三角形全等;
③ 斜边和斜边上的高分别相等的两个直角三角形全等;
④ 两边和第三条边上的高分别相等的两个三角形全等;
⑤ 底边和一腰上的中线分别相等的两个等腰三角形全等.
①③⑤
答案:(1)证明:∵AD和A'D'分别是△ABC和△A'B'C'的中线,BC=B'C',
∴BD=B'D',DC=D'C'。
在△ABD和△A'B'D'中,
AB=A'B',AD=A'D',BD=B'D',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'。
在△ABC和△A'B'C'中,
AB=A'B',∠B=∠B',BC=B'C',
∴△ABC≌△A'B'C'(SAS)。
(2)△ABC≌△A'B'C'。理由如下:
延长AD至点E,使DE=AD,连接BE;延长A'D'至点E',使D'E'=A'D',连接B'E'。
∵AD是△ABC的中线,
∴BD=DC。
在△ADC和△EDB中,
AD=ED,∠ADC=∠EDB,DC=BD,
∴△ADC≌△EDB(SAS),
∴AC=EB。
同理可得A'C'=E'B'。
∵AC=A'C',
∴EB=E'B'。
∵AD=A'D',
∴AE=A'E'。
在△ABE和△A'B'E'中,
AB=A'B',BE=B'E',AE=A'E',
∴△ABE≌△A'B'E'(SSS),
∴∠BAE=∠B'A'E',∠E=∠E'。
∵∠E=∠CAD,∠E'=∠C'A'D',
∴∠CAD=∠C'A'D',
∴∠BAC=∠B'A'C'。
在△ABC和△A'B'C'中,
AB=A'B',∠BAC=∠B'A'C',AC=A'C',
∴△ABC≌△A'B'C'(SAS)。
(3)①③⑤
∴BD=B'D',DC=D'C'。
在△ABD和△A'B'D'中,
AB=A'B',AD=A'D',BD=B'D',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'。
在△ABC和△A'B'C'中,
AB=A'B',∠B=∠B',BC=B'C',
∴△ABC≌△A'B'C'(SAS)。
(2)△ABC≌△A'B'C'。理由如下:
延长AD至点E,使DE=AD,连接BE;延长A'D'至点E',使D'E'=A'D',连接B'E'。
∵AD是△ABC的中线,
∴BD=DC。
在△ADC和△EDB中,
AD=ED,∠ADC=∠EDB,DC=BD,
∴△ADC≌△EDB(SAS),
∴AC=EB。
同理可得A'C'=E'B'。
∵AC=A'C',
∴EB=E'B'。
∵AD=A'D',
∴AE=A'E'。
在△ABE和△A'B'E'中,
AB=A'B',BE=B'E',AE=A'E',
∴△ABE≌△A'B'E'(SSS),
∴∠BAE=∠B'A'E',∠E=∠E'。
∵∠E=∠CAD,∠E'=∠C'A'D',
∴∠CAD=∠C'A'D',
∴∠BAC=∠B'A'C'。
在△ABC和△A'B'C'中,
AB=A'B',∠BAC=∠B'A'C',AC=A'C',
∴△ABC≌△A'B'C'(SAS)。
(3)①③⑤