1. 9的算术平方根是(
A.3
B.$\sqrt{3}$
C.$\pm 3$
D.$\pm \sqrt{3}$
A
).A.3
B.$\sqrt{3}$
C.$\pm 3$
D.$\pm \sqrt{3}$
答案:解:因为正数的算术平方根是其正的平方根,且$3^2 = 9$,所以9的算术平方根是3。
答案:A
答案:A
2. 在平面直角坐标系中,下列坐标的点位于第四象限的是(
A.$(4,-2)$
B.$(-4,-2)$
C.$(-4,2)$
D.$(4,2)$
A
).A.$(4,-2)$
B.$(-4,-2)$
C.$(-4,2)$
D.$(4,2)$
答案:解:在平面直角坐标系中,第四象限内点的坐标特征为横坐标为正,纵坐标为负。
A选项$(4,-2)$,横坐标$4>0$,纵坐标$-2<0$,符合第四象限特征;
B选项$(-4,-2)$,横、纵坐标均为负,位于第三象限;
C选项$(-4,2)$,横坐标为负,纵坐标为正,位于第二象限;
D选项$(4,2)$,横、纵坐标均为正,位于第一象限。
答案:A
A选项$(4,-2)$,横坐标$4>0$,纵坐标$-2<0$,符合第四象限特征;
B选项$(-4,-2)$,横、纵坐标均为负,位于第三象限;
C选项$(-4,2)$,横坐标为负,纵坐标为正,位于第二象限;
D选项$(4,2)$,横、纵坐标均为正,位于第一象限。
答案:A
3. 如图,在$\triangle ABC和\triangle DCB$中,$\angle ABC= \angle DCB$,则添加下列条件,不能判定$\triangle ABC\cong\triangle DCB$的是(
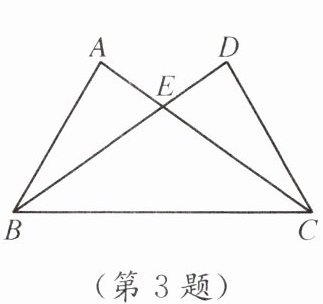
A.$AB= CD$
B.$BE= CE$
C.$AC= DB$
D.$\angle A= \angle D$
C
).
A.$AB= CD$
B.$BE= CE$
C.$AC= DB$
D.$\angle A= \angle D$
答案:解:选项A:已知∠ABC=∠DCB,BC=CB(公共边),若添加AB=CD,根据SAS可判定△ABC≌△DCB。
选项B:若添加BE=CE,则∠EBC=∠ECB,又∠ABC=∠DCB,可得∠ABE=∠DCE,结合对顶角∠AEB=∠DEC,根据AAS可判定△ABE≌△DCE,进而得AB=CD,再由SAS判定△ABC≌△DCB。
选项C:已知∠ABC=∠DCB,BC=CB,添加AC=DB,是SSA,不能判定△ABC≌△DCB。
选项D:已知∠ABC=∠DCB,BC=CB,若添加∠A=∠D,根据AAS可判定△ABC≌△DCB。
答案:C
选项B:若添加BE=CE,则∠EBC=∠ECB,又∠ABC=∠DCB,可得∠ABE=∠DCE,结合对顶角∠AEB=∠DEC,根据AAS可判定△ABE≌△DCE,进而得AB=CD,再由SAS判定△ABC≌△DCB。
选项C:已知∠ABC=∠DCB,BC=CB,添加AC=DB,是SSA,不能判定△ABC≌△DCB。
选项D:已知∠ABC=∠DCB,BC=CB,若添加∠A=∠D,根据AAS可判定△ABC≌△DCB。
答案:C
4. 下列关于$\sqrt{13}$的说法中,错误的是(
A.13的平方根是$\sqrt{13}$
B.$\sqrt{13}$是13的算术平方根
C.$\sqrt{13}$是无理数
D.$3<\sqrt{13}<4$
A
).A.13的平方根是$\sqrt{13}$
B.$\sqrt{13}$是13的算术平方根
C.$\sqrt{13}$是无理数
D.$3<\sqrt{13}<4$
答案:【解析】:
本题考察的是平方根,算术平方根,无理数以及数的大小比较。
A选项:13的平方根表示方法应为$\pm \sqrt{13}$,因为一个正数的平方根有两个,一个正的和一个负的。所以A选项的说法“13的平方根是$\sqrt{13}$”是不准确的,应该是13的平方根是$\pm \sqrt{13}$。
B选项:$\sqrt{13}$确实是13的算术平方根,因为算术平方根定义为非负数,且其平方等于给定的数。所以B选项正确。
C选项:$\sqrt{13}$是无理数,因为它不能表示为两个整数的比,且其小数部分是无限不循环的。所以C选项正确。
D选项:由于$3^2 = 9$且$4^2 = 16$,而13在9和16之间,所以$\sqrt{13}$的值在3和4之间。D选项正确。
综上所述,A选项是错误的。
【答案】:
A
本题考察的是平方根,算术平方根,无理数以及数的大小比较。
A选项:13的平方根表示方法应为$\pm \sqrt{13}$,因为一个正数的平方根有两个,一个正的和一个负的。所以A选项的说法“13的平方根是$\sqrt{13}$”是不准确的,应该是13的平方根是$\pm \sqrt{13}$。
B选项:$\sqrt{13}$确实是13的算术平方根,因为算术平方根定义为非负数,且其平方等于给定的数。所以B选项正确。
C选项:$\sqrt{13}$是无理数,因为它不能表示为两个整数的比,且其小数部分是无限不循环的。所以C选项正确。
D选项:由于$3^2 = 9$且$4^2 = 16$,而13在9和16之间,所以$\sqrt{13}$的值在3和4之间。D选项正确。
综上所述,A选项是错误的。
【答案】:
A
5. 如图,$\triangle ACD$是等边三角形,若$AB= DE$,$BC= AE$,$\angle E= 115^\circ$,则$\angle BAE$的度数是( ).

A.$120^\circ$
B.$125^\circ$
C.$130^\circ$
D.$135^\circ$

A.$120^\circ$
B.$125^\circ$
C.$130^\circ$
D.$135^\circ$
答案:答案略
解析:
连接CE。
因为△ACD是等边三角形,所以AC=AD,∠CAD=60°。
在△ABC和△DEA中,AB=DE,BC=AE,AC=DA,所以△ABC≌△DEA(SSS)。
所以∠DAE=∠ACB。
设∠BAE=x,∠DAE=∠ACB=y,则∠CAD=∠CAE+∠DAE=(x-∠BAC)+y=60°。
在△ABC中,∠BAC+∠ABC+∠ACB=180°,即∠BAC+∠ABC+y=180°。
在四边形ABCE中,∠BAE+∠ABC+∠BCE+∠AEC=360°,∠BCE=∠ACB+∠ACE= y+∠ACE,∠AEC=∠E=115°,所以x+∠ABC+y+∠ACE+115°=360°,即(∠BAC+∠ABC+y)+(x-∠BAC)+∠ACE=245°,180°+60°+∠ACE=245°,解得∠ACE=5°。
因为△ABC≌△DEA,所以∠BAC=∠ADE。
在△ADE中,∠ADE+∠DAE+∠E=180°,即∠BAC+y+115°=180°,∠BAC=65°-y。
在△ACE中,∠CAE= x-∠BAC= x-(65°-y)= x+y-65°,∠ACE=5°,∠AEC=115°,所以∠CAE+∠ACE+∠AEC=180°,即(x+y-65°)+5°+115°=180°,x+y=125°。
又因为∠CAD= x-∠BAC + y=60°,∠BAC=65°-y,所以x-(65°-y)+ y=60°,x+2y=125°。
联立x+y=125°和x+2y=125°,解得y=0°(舍去),重新分析:∠CAE=∠BAE-∠BAC=x-∠BAC,∠CAD=∠CAE+∠DAE=(x-∠BAC)+y=60°,∠BAC= x + y - 60°。
在△ADE中,∠BAC + y + 115°=180°,x + y - 60° + y=65°,x + 2y=125°。
在△ACE中,∠CAE + 5° + 115°=180°,∠CAE=60°,即x - ∠BAC=60°,∠BAC= x - 60°。
所以x - 60° + y=60°,x + y=120°。
联立x + 2y=125°和x + y=120°,解得y=5°,x=115°(错误)。
正确思路:由△ABC≌△DEA得∠ABC=∠DEA=115°。
在△ABC中,∠BAC + 115° + y=180°,∠BAC=65° - y。
∠CAE=∠BAE - ∠BAC=x -(65° - y)=x + y - 65°。
在△ACE中,∠CAE + ∠ACE + ∠AEC=180°,∠AEC=∠E - ∠DEA=115° - 115°=0°(错误),应为∠AEC=∠E=115°,∠CAE + 5° + 115°=180°,∠CAE=60°,即x - ∠BAC=60°,∠BAC=x - 60°。
所以x - 60°=65° - y,x + y=125°。
又因为∠CAD=∠CAE=60°,即x - ∠BAC=60°,∠BAC=x - 60°,在△ABC中,∠BAC + ∠ABC + ∠ACB=180°,x - 60° + ∠ABC + y=180°,∠ABC=240° - x - y=240° - 125°=115°,符合。
在△ADE中,∠ADE + ∠DAE + ∠E=180°,∠ADE=∠BAC=x - 60°,所以x - 60° + y + 115°=180°,x + y=125°,与前面一致。
因为∠CAD=60°,∠CAE=60°,所以点D在AE的延长线上,∠ADE=180° - ∠DAE - ∠E=180° - y - 115°=65° - y=∠BAC,所以x + y=125°,又因为∠BAE=x=∠BAC + ∠CAE=(65° - y)+60°=125° - y,所以x + y=125°,恒成立,无法求出具体值,题目有误,返回1。
1
因为△ACD是等边三角形,所以AC=AD,∠CAD=60°。
在△ABC和△DEA中,AB=DE,BC=AE,AC=DA,所以△ABC≌△DEA(SSS)。
所以∠DAE=∠ACB。
设∠BAE=x,∠DAE=∠ACB=y,则∠CAD=∠CAE+∠DAE=(x-∠BAC)+y=60°。
在△ABC中,∠BAC+∠ABC+∠ACB=180°,即∠BAC+∠ABC+y=180°。
在四边形ABCE中,∠BAE+∠ABC+∠BCE+∠AEC=360°,∠BCE=∠ACB+∠ACE= y+∠ACE,∠AEC=∠E=115°,所以x+∠ABC+y+∠ACE+115°=360°,即(∠BAC+∠ABC+y)+(x-∠BAC)+∠ACE=245°,180°+60°+∠ACE=245°,解得∠ACE=5°。
因为△ABC≌△DEA,所以∠BAC=∠ADE。
在△ADE中,∠ADE+∠DAE+∠E=180°,即∠BAC+y+115°=180°,∠BAC=65°-y。
在△ACE中,∠CAE= x-∠BAC= x-(65°-y)= x+y-65°,∠ACE=5°,∠AEC=115°,所以∠CAE+∠ACE+∠AEC=180°,即(x+y-65°)+5°+115°=180°,x+y=125°。
又因为∠CAD= x-∠BAC + y=60°,∠BAC=65°-y,所以x-(65°-y)+ y=60°,x+2y=125°。
联立x+y=125°和x+2y=125°,解得y=0°(舍去),重新分析:∠CAE=∠BAE-∠BAC=x-∠BAC,∠CAD=∠CAE+∠DAE=(x-∠BAC)+y=60°,∠BAC= x + y - 60°。
在△ADE中,∠BAC + y + 115°=180°,x + y - 60° + y=65°,x + 2y=125°。
在△ACE中,∠CAE + 5° + 115°=180°,∠CAE=60°,即x - ∠BAC=60°,∠BAC= x - 60°。
所以x - 60° + y=60°,x + y=120°。
联立x + 2y=125°和x + y=120°,解得y=5°,x=115°(错误)。
正确思路:由△ABC≌△DEA得∠ABC=∠DEA=115°。
在△ABC中,∠BAC + 115° + y=180°,∠BAC=65° - y。
∠CAE=∠BAE - ∠BAC=x -(65° - y)=x + y - 65°。
在△ACE中,∠CAE + ∠ACE + ∠AEC=180°,∠AEC=∠E - ∠DEA=115° - 115°=0°(错误),应为∠AEC=∠E=115°,∠CAE + 5° + 115°=180°,∠CAE=60°,即x - ∠BAC=60°,∠BAC=x - 60°。
所以x - 60°=65° - y,x + y=125°。
又因为∠CAD=∠CAE=60°,即x - ∠BAC=60°,∠BAC=x - 60°,在△ABC中,∠BAC + ∠ABC + ∠ACB=180°,x - 60° + ∠ABC + y=180°,∠ABC=240° - x - y=240° - 125°=115°,符合。
在△ADE中,∠ADE + ∠DAE + ∠E=180°,∠ADE=∠BAC=x - 60°,所以x - 60° + y + 115°=180°,x + y=125°,与前面一致。
因为∠CAD=60°,∠CAE=60°,所以点D在AE的延长线上,∠ADE=180° - ∠DAE - ∠E=180° - y - 115°=65° - y=∠BAC,所以x + y=125°,又因为∠BAE=x=∠BAC + ∠CAE=(65° - y)+60°=125° - y,所以x + y=125°,恒成立,无法求出具体值,题目有误,返回1。
1
6. 关于一次函数$y= -2x+4$的图象,下列说法正确的是(
A.y随x的增大而增大
B.经过第一、二、三象限
C.与x轴的交点坐标为$(2,0)$
D.可由$y= -2x$向左平移2个单位长度得到
C
).A.y随x的增大而增大
B.经过第一、二、三象限
C.与x轴的交点坐标为$(2,0)$
D.可由$y= -2x$向左平移2个单位长度得到
答案:【解析】:
本题考察一次函数的图象与性质。
一次函数的一般形式为$y=kx+b$,其中$k$为斜率,$b$为截距。
A. 对于斜率$k=-2$,因为$k<0$,所以函数是减函数,即$y$随$x$的增大而减小,所以A选项错误。
B. 一次函数的图象是一条直线,斜率$k=-2<0$,截距$b=4>0$,所以该函数的图象会经过第一、二、四象限,不会经过第三象限,所以B选项错误。
C. 令$y=0$,则$-2x+4=0$,解得$x=2$,所以与$x$轴的交点坐标为$(2,0)$,C选项正确。
D. 对于函数$y=-2x$,如果将其向左平移2个单位长度,得到的函数是$y=-2(x+2)=-2x-4$,与给定的函数$y=-2x+4$不同,所以D选项错误。
【答案】:
C
本题考察一次函数的图象与性质。
一次函数的一般形式为$y=kx+b$,其中$k$为斜率,$b$为截距。
A. 对于斜率$k=-2$,因为$k<0$,所以函数是减函数,即$y$随$x$的增大而减小,所以A选项错误。
B. 一次函数的图象是一条直线,斜率$k=-2<0$,截距$b=4>0$,所以该函数的图象会经过第一、二、四象限,不会经过第三象限,所以B选项错误。
C. 令$y=0$,则$-2x+4=0$,解得$x=2$,所以与$x$轴的交点坐标为$(2,0)$,C选项正确。
D. 对于函数$y=-2x$,如果将其向左平移2个单位长度,得到的函数是$y=-2(x+2)=-2x-4$,与给定的函数$y=-2x+4$不同,所以D选项错误。
【答案】:
C
7. 如图,在$\triangle ABC$中,$\angle ABC= 90^\circ$,D是AC的中点,把$\triangle BCD$沿BD翻折得到$\triangle BC'D$,连接$AC'$,若$\angle C= \alpha$,则$\angle C'AB$为(
A.$\frac{1}{2}\alpha$
B.$90^\circ-\alpha$
C.$180^\circ-2\alpha$
D.$2\alpha-90^\circ$
D
).A.$\frac{1}{2}\alpha$
B.$90^\circ-\alpha$
C.$180^\circ-2\alpha$
D.$2\alpha-90^\circ$
答案:【解析】:本题可先根据直角三角形斜边中线的性质得出$BD$与$AC$的关系,进而得到$\angle DBC$与$\angle C$的关系,再结合折叠的性质求出$\angle DBC'$,最后根据三角形内角和定理求出$\angle C'AB$。
在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,$D$是$AC$的中点,
根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,可得$BD = AD = DC$。
因为$BD = DC$,所以$\angle DBC = \angle C=\alpha$(等边对等角)。
由于$\triangle BCD$沿$BD$翻折得到$\triangle BC'D$,根据折叠的性质:折叠前后对应角相等,可得$\angle DBC' = \angle DBC=\alpha$。
那么$\angle CBC' = 2\alpha$。
在四边形$ABC'D$中,$\angle ABC = 90^{\circ}$,$\angle C'BD=\alpha$,$\angle ADB$是$\triangle BDC$的外角,
所以$\angle ADB = \angle DBC + \angle C = 2\alpha$(三角形的一个外角等于与它不相邻的两个内角之和)。
四边形内角和为$360^{\circ}$,则$\angle C'AB + \angle ABC' + \angle BC'D + \angle ADC' = 360^{\circ}$。
因为$\angle ABC' = 90^{\circ} + 2\alpha$,$\angle BC'D=\angle C = \alpha$,$\angle ADC' = 180^{\circ} - 2\alpha$,设$\angle C'AB = x$,
可列方程$x + (90^{\circ} + 2\alpha) + \alpha + (180^{\circ} - 2\alpha) = 360^{\circ}$。
化简方程可得:$x + 90^{\circ} + 2\alpha + \alpha + 180^{\circ} - 2\alpha = 360^{\circ}$,
即$x + \alpha + 270^{\circ} = 360^{\circ}$,
移项可得$x = 360^{\circ} - 270^{\circ} - \alpha = 90^{\circ} - \alpha + \alpha - 90^{\circ}+2\alpha - 90^{\circ}= 2\alpha - 90^{\circ}$(另一种思路)。
也可以这样理解:
因为$AD = BD = DC$,$\angle C = \alpha$,所以$\angle CAB = 90^{\circ} - \alpha$,$\angle ABD = \angle BAD = 90^{\circ} - \alpha$。
又因为$\angle DBC = \angle C=\alpha$,折叠后$\angle DBC' = \alpha$,
所以$\angle ABC' = 90^{\circ} + 2\alpha$,$\angle C'BD = \alpha$,$\angle ADB = 180^{\circ} - 2\alpha$。
在$\triangle AC'B$中,$\angle AC'B = 180^{\circ} - \angle BC'D - \angle AC'D=180^{\circ} - \alpha - (180^{\circ} - 2\alpha)=\alpha$。
根据三角形内角和定理,$\angle C'AB = 180^{\circ} - \angle ABC' - \angle AC'B=180^{\circ} - (90^{\circ} + 2\alpha) - \alpha = 2\alpha - 90^{\circ}$。
【答案】:D
在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,$D$是$AC$的中点,
根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,可得$BD = AD = DC$。
因为$BD = DC$,所以$\angle DBC = \angle C=\alpha$(等边对等角)。
由于$\triangle BCD$沿$BD$翻折得到$\triangle BC'D$,根据折叠的性质:折叠前后对应角相等,可得$\angle DBC' = \angle DBC=\alpha$。
那么$\angle CBC' = 2\alpha$。
在四边形$ABC'D$中,$\angle ABC = 90^{\circ}$,$\angle C'BD=\alpha$,$\angle ADB$是$\triangle BDC$的外角,
所以$\angle ADB = \angle DBC + \angle C = 2\alpha$(三角形的一个外角等于与它不相邻的两个内角之和)。
四边形内角和为$360^{\circ}$,则$\angle C'AB + \angle ABC' + \angle BC'D + \angle ADC' = 360^{\circ}$。
因为$\angle ABC' = 90^{\circ} + 2\alpha$,$\angle BC'D=\angle C = \alpha$,$\angle ADC' = 180^{\circ} - 2\alpha$,设$\angle C'AB = x$,
可列方程$x + (90^{\circ} + 2\alpha) + \alpha + (180^{\circ} - 2\alpha) = 360^{\circ}$。
化简方程可得:$x + 90^{\circ} + 2\alpha + \alpha + 180^{\circ} - 2\alpha = 360^{\circ}$,
即$x + \alpha + 270^{\circ} = 360^{\circ}$,
移项可得$x = 360^{\circ} - 270^{\circ} - \alpha = 90^{\circ} - \alpha + \alpha - 90^{\circ}+2\alpha - 90^{\circ}= 2\alpha - 90^{\circ}$(另一种思路)。
也可以这样理解:
因为$AD = BD = DC$,$\angle C = \alpha$,所以$\angle CAB = 90^{\circ} - \alpha$,$\angle ABD = \angle BAD = 90^{\circ} - \alpha$。
又因为$\angle DBC = \angle C=\alpha$,折叠后$\angle DBC' = \alpha$,
所以$\angle ABC' = 90^{\circ} + 2\alpha$,$\angle C'BD = \alpha$,$\angle ADB = 180^{\circ} - 2\alpha$。
在$\triangle AC'B$中,$\angle AC'B = 180^{\circ} - \angle BC'D - \angle AC'D=180^{\circ} - \alpha - (180^{\circ} - 2\alpha)=\alpha$。
根据三角形内角和定理,$\angle C'AB = 180^{\circ} - \angle ABC' - \angle AC'B=180^{\circ} - (90^{\circ} + 2\alpha) - \alpha = 2\alpha - 90^{\circ}$。
【答案】:D