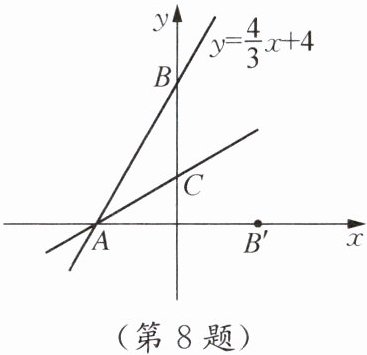
8. 如图,一次函数$y= \frac{4}{3}x+4$的图象分别与x轴、y轴交于点A,B,点C在y轴的正半轴上,若点B关于直线AC的对称点$B'$恰好落在x轴上,则直线AC所对应的函数表达式为(
A.$y= \frac{2}{3}x+\frac{3}{2}$
B.$y= \frac{2}{3}x+\frac{4}{3}$
C.$y= \frac{1}{2}x+\frac{4}{3}$
D.$y= \frac{1}{2}x+\frac{3}{2}$
D
).
A.$y= \frac{2}{3}x+\frac{3}{2}$
B.$y= \frac{2}{3}x+\frac{4}{3}$
C.$y= \frac{1}{2}x+\frac{4}{3}$
D.$y= \frac{1}{2}x+\frac{3}{2}$
答案:解:对于一次函数$y=\frac{4}{3}x + 4$,
令$x=0$,得$y=4$,则$B(0,4)$;
令$y=0$,得$\frac{4}{3}x + 4=0$,解得$x=-3$,则$A(-3,0)$。
设$B'(m,0)$,点$C(0,n)$,$n>0$。
因为点$B$与$B'$关于直线$AC$对称,所以$AC$垂直平分$BB'$。
$BB'$中点坐标为$(\frac{m}{2},2)$,该点在直线$AC$上。
直线$AC$过$A(-3,0)$,$C(0,n)$,其斜率为$\frac{n - 0}{0 - (-3)}=\frac{n}{3}$,函数表达式为$y=\frac{n}{3}x + n$。
将中点$(\frac{m}{2},2)$代入,得$2=\frac{n}{3}\cdot\frac{m}{2} + n$,即$mn + 6n = 12$ ①。
直线$BB'$的斜率为$\frac{0 - 4}{m - 0}=-\frac{4}{m}$,因为$AC\perp BB'$,所以$\frac{n}{3}\cdot(-\frac{4}{m})=-1$,即$4n = 3m$ ②。
由对称知$AB' = AB$,$AB=\sqrt{(-3 - 0)^2 + (0 - 4)^2}=5$,则$AB'=|m - (-3)|=|m + 3|=5$。
因为$B'$在$x$轴正半轴(由图可知),所以$m + 3=5$,$m=2$。
将$m=2$代入②,得$4n=3×2$,$n=\frac{3}{2}$。
所以直线$AC$的表达式为$y=\frac{\frac{3}{2}}{3}x + \frac{3}{2}=\frac{1}{2}x + \frac{3}{2}$。
答案:D
令$x=0$,得$y=4$,则$B(0,4)$;
令$y=0$,得$\frac{4}{3}x + 4=0$,解得$x=-3$,则$A(-3,0)$。
设$B'(m,0)$,点$C(0,n)$,$n>0$。
因为点$B$与$B'$关于直线$AC$对称,所以$AC$垂直平分$BB'$。
$BB'$中点坐标为$(\frac{m}{2},2)$,该点在直线$AC$上。
直线$AC$过$A(-3,0)$,$C(0,n)$,其斜率为$\frac{n - 0}{0 - (-3)}=\frac{n}{3}$,函数表达式为$y=\frac{n}{3}x + n$。
将中点$(\frac{m}{2},2)$代入,得$2=\frac{n}{3}\cdot\frac{m}{2} + n$,即$mn + 6n = 12$ ①。
直线$BB'$的斜率为$\frac{0 - 4}{m - 0}=-\frac{4}{m}$,因为$AC\perp BB'$,所以$\frac{n}{3}\cdot(-\frac{4}{m})=-1$,即$4n = 3m$ ②。
由对称知$AB' = AB$,$AB=\sqrt{(-3 - 0)^2 + (0 - 4)^2}=5$,则$AB'=|m - (-3)|=|m + 3|=5$。
因为$B'$在$x$轴正半轴(由图可知),所以$m + 3=5$,$m=2$。
将$m=2$代入②,得$4n=3×2$,$n=\frac{3}{2}$。
所以直线$AC$的表达式为$y=\frac{\frac{3}{2}}{3}x + \frac{3}{2}=\frac{1}{2}x + \frac{3}{2}$。
答案:D
9. 下列五个数$-\frac{3}{7},3.1415926,\sqrt{3},\sqrt{4},2\pi$,其中无理数有
2
个.答案:解:无理数是无限不循环小数。
$-\frac{3}{7}$是分数,属于有理数;
$3.1415926$是有限小数,属于有理数;
$\sqrt{3}$是无限不循环小数,属于无理数;
$\sqrt{4}=2$是整数,属于有理数;
$2\pi$是无限不循环小数,属于无理数。
综上,无理数有$\sqrt{3},2\pi$,共2个。
答案:2
$-\frac{3}{7}$是分数,属于有理数;
$3.1415926$是有限小数,属于有理数;
$\sqrt{3}$是无限不循环小数,属于无理数;
$\sqrt{4}=2$是整数,属于有理数;
$2\pi$是无限不循环小数,属于无理数。
综上,无理数有$\sqrt{3},2\pi$,共2个。
答案:2
10. 与$\sqrt{20}$最接近的整数是
4
.答案:解:$\sqrt{16} = 4$,$\sqrt{25} = 5$,
$\because 16 < 20 < 25$,
$\therefore 4 < \sqrt{20} < 5$,
$20 - 16 = 4$,$25 - 20 = 5$,
$\because 4 < 5$,
$\therefore \sqrt{20}$更接近$4$。
答案:$4$
$\because 16 < 20 < 25$,
$\therefore 4 < \sqrt{20} < 5$,
$20 - 16 = 4$,$25 - 20 = 5$,
$\because 4 < 5$,
$\therefore \sqrt{20}$更接近$4$。
答案:$4$
11. 将一次函数$y= 3x-4的图象平移后经过点A(2,-1)$,则平移后图象的函数表达式为______
$y = 3x - 7$
.答案:解:设平移后一次函数的表达式为$y = 3x + b$。
因为平移后的图象经过点$A(2, -1)$,
所以将$x = 2$,$y = -1$代入$y = 3x + b$,
得$-1 = 3×2 + b$,
即$-1 = 6 + b$,
解得$b = -7$。
故平移后图象的函数表达式为$y = 3x - 7$。
因为平移后的图象经过点$A(2, -1)$,
所以将$x = 2$,$y = -1$代入$y = 3x + b$,
得$-1 = 3×2 + b$,
即$-1 = 6 + b$,
解得$b = -7$。
故平移后图象的函数表达式为$y = 3x - 7$。
12. 如图,线段AB,BC的垂直平分线$l_1,l_2$相交于点O,若$\angle AOC= 90^\circ$,$\angle A= 13^\circ$,则$\angle C= $______°.


37
答案:解:连接OB。
∵l₁是AB的垂直平分线,
∴OA=OB,∠OAB=∠OBA=13°。
∵l₂是BC的垂直平分线,
∴OB=OC,∠OBC=∠OCB。
设∠C=∠OCB=x,则∠OBC=x。
在△AOB中,∠AOB=180°-2×13°=154°。
在△BOC中,∠BOC=180°-2x。
∵∠AOB+∠BOC-∠AOC=360°(周角定义),∠AOC=90°,
∴154°+(180°-2x)-90°=360°,
解得x=37°。
37
∵l₁是AB的垂直平分线,
∴OA=OB,∠OAB=∠OBA=13°。
∵l₂是BC的垂直平分线,
∴OB=OC,∠OBC=∠OCB。
设∠C=∠OCB=x,则∠OBC=x。
在△AOB中,∠AOB=180°-2×13°=154°。
在△BOC中,∠BOC=180°-2x。
∵∠AOB+∠BOC-∠AOC=360°(周角定义),∠AOC=90°,
∴154°+(180°-2x)-90°=360°,
解得x=37°。
37
13. 一次函数$y= kx+b$的图象如图所示,则关于x的不等式$kx+2b<0$的解集是
$x>6$
.答案:解:由图可知,一次函数$y=kx+b$的图象与x轴交于点$(3,0)$,且y随x的增大而减小,所以$k<0$。
将$(3,0)$代入$y=kx+b$,得$3k+b=0$,即$b=-3k$。
不等式$kx+2b<0$可化为$kx+2(-3k)<0$,即$kx-6k<0$。
因为$k<0$,两边同时除以k,不等号方向改变,得$x-6>0$,解得$x>6$。
故答案为$x>6$。
将$(3,0)$代入$y=kx+b$,得$3k+b=0$,即$b=-3k$。
不等式$kx+2b<0$可化为$kx+2(-3k)<0$,即$kx-6k<0$。
因为$k<0$,两边同时除以k,不等号方向改变,得$x-6>0$,解得$x>6$。
故答案为$x>6$。
14. 在$\triangle ABC$中,$\angle ABC= 30^\circ$,$AB= 6$,$BC= 2$,以AC为边作等边三角形ACD,连接BD,则$BD^2$的值为______
40
.答案:1. 首先,利用余弦定理求$AC^{2}$:
在$\triangle ABC$中,根据余弦定理$AC^{2}=AB^{2}+BC^{2}-2AB\cdot BC\cdot\cos\angle ABC$。
已知$AB = 6$,$BC = 2$,$\angle ABC = 30^{\circ}$,$\cos30^{\circ}=\frac{\sqrt{3}}{2}$。
则$AC^{2}=6^{2}+2^{2}-2×6×2×\frac{\sqrt{3}}{2}=36 + 4-12\sqrt{3}=40 - 12\sqrt{3}$。
同时$\sin30^{\circ}=\frac{1}{2}$,根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC\cdot\sin\angle ABC=\frac{1}{2}×6×2×\frac{1}{2}=3$。
2. 然后,将$\triangle ABD$绕点$A$逆时针旋转$60^{\circ}$:
因为$\triangle ACD$是等边三角形,$AD = AC$,$\angle CAD = 60^{\circ}$。
设$\angle BAC=\alpha$,则$\angle BAD=\alpha + 60^{\circ}$,旋转后$AB$与$AC$重合(设$B$旋转到$B'$),$AB'=AB = 6$,$\angle B'AB = 60^{\circ}$,$B'C = BD$。
此时$\triangle ABB'$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形,$AB = AB'$,$\angle B'AB = 60^{\circ}$),所以$BB'=AB = 6$,$\angle AB'B = 60^{\circ}$。
又$\angle ABC = 30^{\circ}$,根据余弦定理$B'C^{2}=BB'^{2}+BC^{2}-2BB'\cdot BC\cdot\cos(\angle AB'B+\angle ABC)$。
3. 最后,计算$B'C^{2}$(即$BD^{2}$):
因为$\angle AB'B+\angle ABC=60^{\circ}+30^{\circ}=90^{\circ}$,$BB' = 6$,$BC = 2$。
根据勾股定理$B'C^{2}=BD^{2}=BB'^{2}+BC^{2}$(因为$\cos90^{\circ}=0$)。
所以$BD^{2}=6^{2}+2^{2}=36 + 4=40$。
故$BD^{2}$的值为$40$。
在$\triangle ABC$中,根据余弦定理$AC^{2}=AB^{2}+BC^{2}-2AB\cdot BC\cdot\cos\angle ABC$。
已知$AB = 6$,$BC = 2$,$\angle ABC = 30^{\circ}$,$\cos30^{\circ}=\frac{\sqrt{3}}{2}$。
则$AC^{2}=6^{2}+2^{2}-2×6×2×\frac{\sqrt{3}}{2}=36 + 4-12\sqrt{3}=40 - 12\sqrt{3}$。
同时$\sin30^{\circ}=\frac{1}{2}$,根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC\cdot\sin\angle ABC=\frac{1}{2}×6×2×\frac{1}{2}=3$。
2. 然后,将$\triangle ABD$绕点$A$逆时针旋转$60^{\circ}$:
因为$\triangle ACD$是等边三角形,$AD = AC$,$\angle CAD = 60^{\circ}$。
设$\angle BAC=\alpha$,则$\angle BAD=\alpha + 60^{\circ}$,旋转后$AB$与$AC$重合(设$B$旋转到$B'$),$AB'=AB = 6$,$\angle B'AB = 60^{\circ}$,$B'C = BD$。
此时$\triangle ABB'$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形,$AB = AB'$,$\angle B'AB = 60^{\circ}$),所以$BB'=AB = 6$,$\angle AB'B = 60^{\circ}$。
又$\angle ABC = 30^{\circ}$,根据余弦定理$B'C^{2}=BB'^{2}+BC^{2}-2BB'\cdot BC\cdot\cos(\angle AB'B+\angle ABC)$。
3. 最后,计算$B'C^{2}$(即$BD^{2}$):
因为$\angle AB'B+\angle ABC=60^{\circ}+30^{\circ}=90^{\circ}$,$BB' = 6$,$BC = 2$。
根据勾股定理$B'C^{2}=BD^{2}=BB'^{2}+BC^{2}$(因为$\cos90^{\circ}=0$)。
所以$BD^{2}=6^{2}+2^{2}=36 + 4=40$。
故$BD^{2}$的值为$40$。
15. 求下列各式中x的值:
(1)$2(x+1)^2= 8$;
(2)$8(x-1)^3= 27$.
(1)$2(x+1)^2= 8$;
(2)$8(x-1)^3= 27$.
答案:(1)解:方程两边同时除以2,得$(x+1)^2=4$,
开平方,得$x+1=\pm2$,
即$x+1=2$或$x+1=-2$,
解得$x=1$或$x=-3$。
(2)解:方程两边同时除以8,得$(x-1)^3=\frac{27}{8}$,
开立方,得$x-1=\frac{3}{2}$,
解得$x=\frac{5}{2}$。
开平方,得$x+1=\pm2$,
即$x+1=2$或$x+1=-2$,
解得$x=1$或$x=-3$。
(2)解:方程两边同时除以8,得$(x-1)^3=\frac{27}{8}$,
开立方,得$x-1=\frac{3}{2}$,
解得$x=\frac{5}{2}$。