16. 计算$\sqrt{(-3)^2}+(\sqrt{2})^2-\sqrt[3]{\frac{1}{8}}$.
答案:【解析】:
本题主要考察平方根、立方根的计算以及基本的算术运算。
首先,我们需要分别计算出每一项的值,然后再进行加减运算。
第一项:$\sqrt{(-3)^2}$,根据平方根的定义,$\sqrt{a^2} = |a|$,所以$\sqrt{(-3)^2} = |-3| = 3$。
第二项:$(\sqrt{2})^2$,根据平方的定义,$(\sqrt{a})^2 = a$,所以$(\sqrt{2})^2 = 2$。
第三项:$\sqrt[3]{\frac{1}{8}}$,根据立方根的定义,$\sqrt[3]{a^3} = a$,所以$\sqrt[3]{\frac{1}{8}} = \frac{1}{2}$,因为$(\frac{1}{2})^3 = \frac{1}{8}$。
最后,将这三项进行加减运算,即$3 + 2 - \frac{1}{2}$。
【答案】:
解:
原式
$= \sqrt{(-3)^2} + (\sqrt{2})^2 - \sqrt[3]{\frac{1}{8}}$
$= 3 + 2 - \frac{1}{2}$
$= 5 - \frac{1}{2}$
$= \frac{10}{2} - \frac{1}{2}$
$= \frac{9}{2}$
所以,原式的值为$\frac{9}{2}$。
本题主要考察平方根、立方根的计算以及基本的算术运算。
首先,我们需要分别计算出每一项的值,然后再进行加减运算。
第一项:$\sqrt{(-3)^2}$,根据平方根的定义,$\sqrt{a^2} = |a|$,所以$\sqrt{(-3)^2} = |-3| = 3$。
第二项:$(\sqrt{2})^2$,根据平方的定义,$(\sqrt{a})^2 = a$,所以$(\sqrt{2})^2 = 2$。
第三项:$\sqrt[3]{\frac{1}{8}}$,根据立方根的定义,$\sqrt[3]{a^3} = a$,所以$\sqrt[3]{\frac{1}{8}} = \frac{1}{2}$,因为$(\frac{1}{2})^3 = \frac{1}{8}$。
最后,将这三项进行加减运算,即$3 + 2 - \frac{1}{2}$。
【答案】:
解:
原式
$= \sqrt{(-3)^2} + (\sqrt{2})^2 - \sqrt[3]{\frac{1}{8}}$
$= 3 + 2 - \frac{1}{2}$
$= 5 - \frac{1}{2}$
$= \frac{10}{2} - \frac{1}{2}$
$= \frac{9}{2}$
所以,原式的值为$\frac{9}{2}$。
17. 如图,用$(-1,-1)$表示点A的位置,用$(3,0)$表示点B的位置.
(1)画出平面直角坐标系.
(2)点E的坐标为______
(3)$\triangle CDE$的面积为______
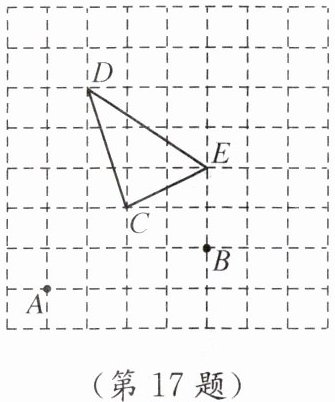
(1)画出平面直角坐标系.
(2)点E的坐标为______
(2,1)
.(3)$\triangle CDE$的面积为______
2
.
答案:
(1) (此处需根据点A(-1,-1)和点B(3,0)在网格中的位置确定坐标系,以点A向右1格、向上1格为原点,水平向右为x轴正方向,竖直向上为y轴正方向建立平面直角坐标系)
(2) (2,1)
(3) 2
(1) (此处需根据点A(-1,-1)和点B(3,0)在网格中的位置确定坐标系,以点A向右1格、向上1格为原点,水平向右为x轴正方向,竖直向上为y轴正方向建立平面直角坐标系)
(2) (2,1)
(3) 2
18. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^\circ$,$\triangle CAP和\triangle CBQ$都是等边三角形,BQ,CP相交于点H.求证:$BQ\perp CP$.


答案:证明:
∵△CAP和△CBQ都是等边三角形,
∴CA=CP,CB=CQ,∠ACP=∠BCQ=60°。
∵∠ACB=90°,
∴∠QCH=∠ACB - ∠BCQ=90° - 60°=30°,
∠PCH=∠ACP + ∠QCH=60° + 30°=90°。
∵∠PCH=90°,
∴BQ⊥CP。
∵△CAP和△CBQ都是等边三角形,
∴CA=CP,CB=CQ,∠ACP=∠BCQ=60°。
∵∠ACB=90°,
∴∠QCH=∠ACB - ∠BCQ=90° - 60°=30°,
∠PCH=∠ACP + ∠QCH=60° + 30°=90°。
∵∠PCH=90°,
∴BQ⊥CP。