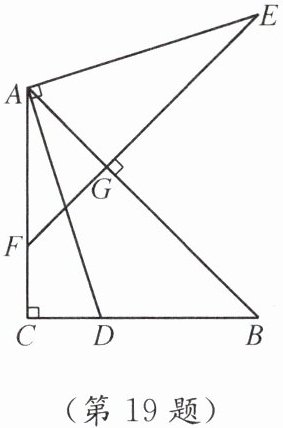
19. 如图,在$\triangle ABC$中,$\angle C= 90^\circ$,$AC= BC$,点D在BC边上,$AE\perp AD$,$AE= AD$,过点E作$EF\perp AB$,分别交边AB,AC于点G,F.
(1)求证:$\triangle EAF\cong\triangle ADB$.
(2)连接DF,求证:$EF= DF+2AG$.
(3)连接ED,若$ED= 10$,$AB= 4AG$,则AG的长为______.

(1)证明：
∵∠C=90°，AC=BC，
∴∠CAB=∠B=45°．
∵EF⊥AB，
∴∠AGF=90°，∠AFG=45°=∠B，
∴AG=FG．
∵AE⊥AD，
∴∠DAE=90°=∠C，
∴∠CAE+∠CAD=∠BAD+∠CAD=90°，
∴∠CAE=∠BAD．
在△EAF和△ADB中，∠EFA=∠B，∠EAF=∠ADB，AE=AD，
∴△EAF≌△ADB(AAS)．
(2)证明：
∵△EAF≌△ADB，
∴AF=BD，EF=AB．
∵AC=BC，CF=AC-AF，CD=BC-BD，
∴CF=CD．
过点D作DH⊥AB于H，
∵∠B=45°，
∴DH=BH，∠DHB=90°=∠AGF．
∵∠C=90°，DH⊥AB，AD=AD，
∴△ACD≌△AHD(HL)，
∴AC=AH，CD=DH=BH=CF．
∵AG=FG，EF=EG+FG=EG+AG，AB=AG+GH+HB，EF=AB，
∴EG=GH+HB，又DF=GH，HB=CF=AG，
∴EF=DF+2AG．
(3)

20. 如图,点A,B是直线CD外的两点,利用直尺与圆规在直线CD上作出符合要求的点P.
(1)$\angle APD= \angle BPD$;
(2)$\angle APD= 2\angle BPD$.