【初步探究】
(1)如图①,当$\triangle OAB与\triangle OCD$无重叠时:
① 若$OA= 2$,$OB= 4$,则OE的范围是;
② 求证:$OE= \frac{1}{2}CD$.

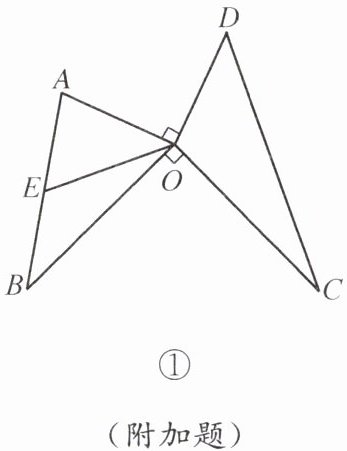
证明：延长 $OE$ 至点 $F$，使 $EF = OE$，连接 $AF$、$BF$。
∵ $E$ 是 $AB$ 中点，∴ 四边形 $AFBO$ 是平行四边形，∴ $AF // OB$，$AF = OB$。
∵ $OB = OC$，∴ $AF = OC$。
∵ $OA \perp OD$，$OB \perp OC$，∴ $\angle AOD = \angle BOC = 90^\circ$，
∴ $\angle AOB + \angle BOD = \angle COD + \angle BOD$，即 $\angle AOB = \angle COD$。
∵ $AF // OB$，∴ $\angle OAF + \angle AOB = 180^\circ$，
又 $\angle OCD + \angle COD = 180^\circ$，∴ $\angle OAF = \angle OCD$。
∵ $OA = OD$，∴ $\triangle OAF \cong \triangle DOC(SAS)$，∴ $OF = CD$，
∵ $OF = 2OE$，∴ $OE = \frac{1}{2}CD$。
【模型再研】
(2)如图②,当$\triangle OAB与\triangle OCD$有重叠时,写出OE与CD所满足的位置关系,并说明理由.

$OE \perp CD$
理由：由(1)②知 $OE = \frac{1}{2}CD$，且 $\triangle OAF \cong \triangle DOC$，
∴ $\angle AOF = \angle ODC$，
∵ $\angle AOD = 90^\circ$，∴ $\angle AOF + \angle FOD = 90^\circ$，
∴ $\angle ODC + \angle FOD = 90^\circ$，∴ $\angle OFD = 90^\circ$，即 $OE \perp CD$。
【结论运用】
(3)已知直线OE与直线CD相交于点F,连接AF,若$OA= 2$,直接写出AF的取值范围.