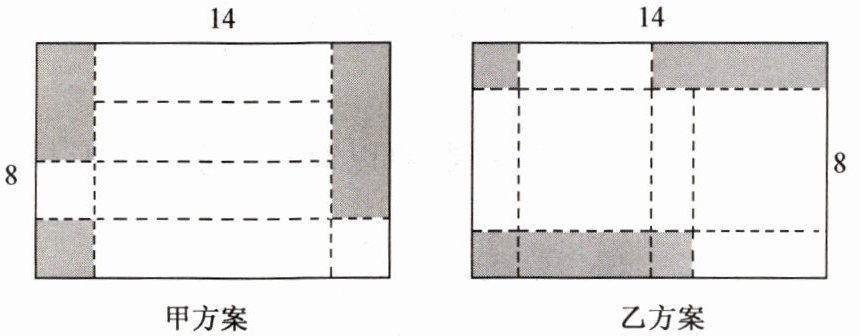
相同规格(长为14,宽为8)的长方形硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,有如图所示的甲、乙两种方案,所得长方体体积分别记为$V_{甲}和V_{乙}$.下列说法正确的是(
A.$V_{甲}>V_{乙}$
B.$V_{甲}= V_{乙}$
C.$V_{甲}<V_{乙}$
D.无法判断
A
)
A.$V_{甲}>V_{乙}$
B.$V_{甲}= V_{乙}$
C.$V_{甲}<V_{乙}$
D.无法判断
答案:A.
解析:
甲方案:
设底面正方形边长为$a$,长方体高为$h_甲$。
由图可知:$2a = 8$,解得$a = 4$。
高$h_甲 = 14 - a = 14 - 4 = 10$。
体积$V_甲 = a^2h_甲 = 4^2 × 10 = 160$。
乙方案:
设底面正方形边长为$b$,长方体高为$h_乙$。
由图可知:$2b = 14$,解得$b = 7$。
高$h_乙 = 8 - b = 8 - 7 = 1$。
体积$V_乙 = b^2h_乙 = 7^2 × 1 = 49$。
比较:
$V_甲 = 160$,$V_乙 = 49$,故$V_甲 > V_乙$。
A.
设底面正方形边长为$a$,长方体高为$h_甲$。
由图可知:$2a = 8$,解得$a = 4$。
高$h_甲 = 14 - a = 14 - 4 = 10$。
体积$V_甲 = a^2h_甲 = 4^2 × 10 = 160$。
乙方案:
设底面正方形边长为$b$,长方体高为$h_乙$。
由图可知:$2b = 14$,解得$b = 7$。
高$h_乙 = 8 - b = 8 - 7 = 1$。
体积$V_乙 = b^2h_乙 = 7^2 × 1 = 49$。
比较:
$V_甲 = 160$,$V_乙 = 49$,故$V_甲 > V_乙$。
A.
1. 圆柱由
3
个面围成,圆锥由______2
个面围成,它们的底面都是______圆
,侧面都是______(选填“曲”或“平”)曲
面.答案:3;2;圆;曲.
2. 五棱柱有
10
个顶点,______15
条棱,______7
个面.答案:10;15;7.
3. 流星划过天空时留下一道明亮的光线,用数学知识解释为
点动成线.
答案:点动成线.
4. 面与面相交成
线
,线与线相交得到点
.答案:线;点.
问题 推理猜测题:
(1)三棱锥有
(2)三棱柱有
(3)
(4)
名师指导
注意棱锥与棱柱的总棱数与底面边数的关系,由简单的开始,把握规律.
解题示范(学生在教师指导下,独立完成)
解:
(1)三棱锥有
6
条棱,四棱锥有8
条棱,十棱锥有20
条棱;(2)三棱柱有
9
条棱,四棱柱有12
条棱,十棱柱有30
条棱;(3)
十五
棱锥有 30 条棱;(4)
二十
棱柱有 60 条棱.名师指导
注意棱锥与棱柱的总棱数与底面边数的关系,由简单的开始,把握规律.
解题示范(学生在教师指导下,独立完成)
解:
答案:(1)
解:三棱锥底面有3条边,从底面每个顶点出发都有一条侧棱到顶点,共3条侧棱,所以三棱锥棱数为底面边数与侧棱数之和,即$3 + 3=6$条;
四棱锥底面有4条边,4条侧棱,棱数为$4 + 4 = 8$条;
设$n$棱锥,底面有$n$条边,$n$条侧棱,棱数为$n + n=2n$条,当$n = 10$时,棱数为$2×10 = 20$条。
故答案为:6;8;20。
(2)
解:三棱柱上下底面共$3+3 = 6$条棱,侧棱有3条,棱数为$6 + 3=9$条;
四棱柱上下底面共$4+4 = 8$条棱,侧棱有4条,棱数为$8 + 4 = 12$条;
设$n$棱柱,上下底面共$2n$条棱,侧棱有$n$条,棱数为$2n + n=3n$条,当$n = 10$时,棱数为$3×10 = 30$条。
故答案为:9;12;30。
(3)
解:设$n$棱锥有30条棱,由$2n = 30$,解得$n = 15$。
故答案为:十五。
(4)
解:设$n$棱柱有60条棱,由$3n = 60$,解得$n = 20$。
故答案为:二十。
解:三棱锥底面有3条边,从底面每个顶点出发都有一条侧棱到顶点,共3条侧棱,所以三棱锥棱数为底面边数与侧棱数之和,即$3 + 3=6$条;
四棱锥底面有4条边,4条侧棱,棱数为$4 + 4 = 8$条;
设$n$棱锥,底面有$n$条边,$n$条侧棱,棱数为$n + n=2n$条,当$n = 10$时,棱数为$2×10 = 20$条。
故答案为:6;8;20。
(2)
解:三棱柱上下底面共$3+3 = 6$条棱,侧棱有3条,棱数为$6 + 3=9$条;
四棱柱上下底面共$4+4 = 8$条棱,侧棱有4条,棱数为$8 + 4 = 12$条;
设$n$棱柱,上下底面共$2n$条棱,侧棱有$n$条,棱数为$2n + n=3n$条,当$n = 10$时,棱数为$3×10 = 30$条。
故答案为:9;12;30。
(3)
解:设$n$棱锥有30条棱,由$2n = 30$,解得$n = 15$。
故答案为:十五。
(4)
解:设$n$棱柱有60条棱,由$3n = 60$,解得$n = 20$。
故答案为:二十。