1. 如图,利用线段的和、差填空:
(1) $ BC = BD - $
(2) $ AC = $
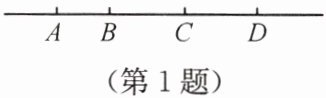
(1) $ BC = BD - $
CD
$ = $AC
$ - AB $;(2) $ AC = $
AB
$ + $BC
$ = $AD
$ - $CD
.
答案:(1)CD,AC;(2)AB,BC;AD,CD
解析:
(1)$CD$,$AC$;
(2)$AB$,$BC$,$AD$,$CD$
(2)$AB$,$BC$,$AD$,$CD$
2. 如图,点 $ C $ 是线段 $ AB $ 的中点,点 $ D $ 是线段 $ BC $ 的中点,下面等式不正确的是(

A.$ CD = AD - BC $
B.$ CD = AC - DB $
C.$ CD = \frac{1}{2}AB - BD $
D.$ CD = \frac{1}{3}AB $
D
)
A.$ CD = AD - BC $
B.$ CD = AC - DB $
C.$ CD = \frac{1}{2}AB - BD $
D.$ CD = \frac{1}{3}AB $
答案:D
解析:
设线段$AB$的长度为$4x$。
因为点$C$是$AB$的中点,所以$AC=CB=\frac{1}{2}AB = 2x$。
因为点$D$是$BC$的中点,所以$CD=DB=\frac{1}{2}BC=x$。
选项A:$AD = AC + CD=2x + x=3x$,$AD - BC=3x - 2x=x=CD$,等式成立。
选项B:$AC - DB=2x - x=x=CD$,等式成立。
选项C:$\frac{1}{2}AB - BD=2x - x=x=CD$,等式成立。
选项D:$\frac{1}{3}AB=\frac{4x}{3}\neq x=CD$,等式不成立。
D
因为点$C$是$AB$的中点,所以$AC=CB=\frac{1}{2}AB = 2x$。
因为点$D$是$BC$的中点,所以$CD=DB=\frac{1}{2}BC=x$。
选项A:$AD = AC + CD=2x + x=3x$,$AD - BC=3x - 2x=x=CD$,等式成立。
选项B:$AC - DB=2x - x=x=CD$,等式成立。
选项C:$\frac{1}{2}AB - BD=2x - x=x=CD$,等式成立。
选项D:$\frac{1}{3}AB=\frac{4x}{3}\neq x=CD$,等式不成立。
D
3. 已知线段 $ AB = 6\ cm $,在直线 $ AB $ 上取一点 $ C $,使 $ BC = 2\ cm $,则线段 $ AB $ 的中点 $ M $ 与 $ AC $ 的中点 $ N $ 的距离为(
A.$ 1\ cm $
B.$ 3\ cm $
C.$ 2\ cm $ 或 $ 3\ cm $
D.$ 1\ cm $ 或 $ 3\ cm $
A
)A.$ 1\ cm $
B.$ 3\ cm $
C.$ 2\ cm $ 或 $ 3\ cm $
D.$ 1\ cm $ 或 $ 3\ cm $
答案:A
解析:
以A为原点,AB方向为正方向建立数轴,A:0,B:6。
情况1:C在B右侧
C:6+2=8,AC=8-0=8。
M为AB中点:$M=\frac{0+6}{2}=3$。
N为AC中点:$N=\frac{0+8}{2}=4$。
$MN=|4-3|=1\ cm$。
情况2:C在B左侧
C:6-2=4,AC=4-0=4。
M:3,N:$\frac{0+4}{2}=2$。
$MN=|3-2|=1\ cm$。
A
情况1:C在B右侧
C:6+2=8,AC=8-0=8。
M为AB中点:$M=\frac{0+6}{2}=3$。
N为AC中点:$N=\frac{0+8}{2}=4$。
$MN=|4-3|=1\ cm$。
情况2:C在B左侧
C:6-2=4,AC=4-0=4。
M:3,N:$\frac{0+4}{2}=2$。
$MN=|3-2|=1\ cm$。
A
4. 下列说法正确的是(
A.连接两点的线段叫作两点间的距离
B.在所有连接两点的线中,直线最短
C.线段 $ AB $ 就是表示点 $ A $ 到点 $ B $ 的距离
D.点 $ A $ 到点 $ B $ 的距离就是线段 $ AB $ 的长度
D
)A.连接两点的线段叫作两点间的距离
B.在所有连接两点的线中,直线最短
C.线段 $ AB $ 就是表示点 $ A $ 到点 $ B $ 的距离
D.点 $ A $ 到点 $ B $ 的距离就是线段 $ AB $ 的长度
答案:D
5. 如图,$ A $,$ B $,$ C $,$ D $,$ E $ 五点在同一条直线上,点 $ D $ 是线段 $ AB $ 的中点,点 $ E $ 是线段 $ BC $ 的中点,若 $ AB = 12 $,$ DE = 4 $,求线段 $ BC $ 的长.


4
答案:4
解析:
因为点$D$是线段$AB$的中点,$AB = 12$,所以$AD=DB=\frac{1}{2}AB = 6$。
由图可知点的顺序为$A$、$D$、$C$、$E$、$B$,则$DE=DB - EB$。
设$BC=x$,因为点$E$是线段$BC$的中点,所以$EB=\frac{1}{2}BC=\frac{x}{2}$。
已知$DE = 4$,$DB = 6$,所以$6-\frac{x}{2}=4$,解得$x = 4$,即$BC=4$。
4
由图可知点的顺序为$A$、$D$、$C$、$E$、$B$,则$DE=DB - EB$。
设$BC=x$,因为点$E$是线段$BC$的中点,所以$EB=\frac{1}{2}BC=\frac{x}{2}$。
已知$DE = 4$,$DB = 6$,所以$6-\frac{x}{2}=4$,解得$x = 4$,即$BC=4$。
4
6. 如图,线段 $ AB = 3 $.
(1) 作图:延长线段 $ AB $ 到点 $ C $,使 $ BC = 2AB $;
(2) 若 $ M $,$ N $ 分别为线段 $ AB $,$ BC $ 的中点,求线段 $ MN $ 的长.

(1) 作图:延长线段 $ AB $ 到点 $ C $,使 $ BC = 2AB $;
(2) 若 $ M $,$ N $ 分别为线段 $ AB $,$ BC $ 的中点,求线段 $ MN $ 的长.

答案:
(1)如图所示,点C为所求.

(2)MN=4.5
(1)如图所示,点C为所求.

(2)MN=4.5