23. (8 分)已知点 B 在线段 AC 上,点 D 在线段 AB 上.
(1)如图①,若 AB = 6 cm,BC = 4 cm,D 为线段 AC 的中点,求线段 DB 的长度;
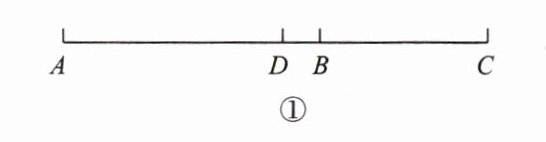
(2)如图②,若 BD = $\frac{1}{4}$AB = $\frac{1}{3}$CD,E 为线段 AB 的中点,EC = 12 cm,求线段 AC 的长度.

(1)如图①,若 AB = 6 cm,BC = 4 cm,D 为线段 AC 的中点,求线段 DB 的长度;

(2)如图②,若 BD = $\frac{1}{4}$AB = $\frac{1}{3}$CD,E 为线段 AB 的中点,EC = 12 cm,求线段 AC 的长度.

答案:
解:(1)如图①所示: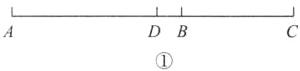
∵AC=AB+BC,AB=6 cm,BC=4 cm
∴AC=6+4=10(cm). 又
∵D 为线段 AC 的中点,
∴DC=$\frac{1}{2}$AC=$\frac{1}{2}$×10=5(cm),
∴DB=DC-BC=5-4=1(cm).(2)如图②所示: 设 BD=x cm,
设 BD=x cm,
∵BD=$\frac{1}{4}$AB=$\frac{1}{3}$CD,
∴AB=4BD=4x cm,CD=3BD=3x cm. 又
∵DC=DB+BC,
∴BC=3x-x=2x(cm). 又
∵AC=AB+BC,
∴AC=4x+2x=6x(cm).
∵E 为线段 AB 的中点,
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$×4x=2x(cm). 又
∵EC=BE+BC,
∴EC=2x+2x=4x(cm). 又
∵EC=12 cm,
∴4x=12,解得 x=3,
∴AC=6x=6×3=18(cm).
解:(1)如图①所示:

∵AC=AB+BC,AB=6 cm,BC=4 cm
∴AC=6+4=10(cm). 又
∵D 为线段 AC 的中点,
∴DC=$\frac{1}{2}$AC=$\frac{1}{2}$×10=5(cm),
∴DB=DC-BC=5-4=1(cm).(2)如图②所示:
 设 BD=x cm,
设 BD=x cm,∵BD=$\frac{1}{4}$AB=$\frac{1}{3}$CD,
∴AB=4BD=4x cm,CD=3BD=3x cm. 又
∵DC=DB+BC,
∴BC=3x-x=2x(cm). 又
∵AC=AB+BC,
∴AC=4x+2x=6x(cm).
∵E 为线段 AB 的中点,
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$×4x=2x(cm). 又
∵EC=BE+BC,
∴EC=2x+2x=4x(cm). 又
∵EC=12 cm,
∴4x=12,解得 x=3,
∴AC=6x=6×3=18(cm).
24. (8 分)如图,∠AOD = $28^{\circ}$,∠AOB 与∠AOD 互余,OC 平分∠AOB,求∠COD 的度数.


答案:3°
解析:
∵∠AOB与∠AOD互余,∠AOD=28°,
∴∠AOB=90°-∠AOD=90°-28°=62°.
∵OC平分∠AOB,
∴∠AOC=∠AOB/2=62°/2=31°.
∴∠COD=∠AOC-∠AOD=31°-28°=3°.
∠COD的度数为3°.
25. (10 分)定义:从一个角的顶点出发,把这个角分成 1 : 2 的两个角的射线,叫作这个角的三分线,显然,一个角的三分线有两条.
(1)如图(1),已知 OC 是∠AOB 的一条三分线,且∠BOC > ∠AOC,若∠AOB = $75^{\circ}$,则∠AOC =
(2)如图(2),已知∠AOB = $90^{\circ}$,若 OC,OD 是∠AOB 的两条三分线.
① 求∠COD 的度数;
② 在①的基础上,现以 O 为中心,将∠COD 顺时针旋转 $n^{\circ}$得到∠C'OD'. 当 OA 恰好是∠C'OD'的三分线时,求 n 的值.
(1)(2)

(1)如图(1),已知 OC 是∠AOB 的一条三分线,且∠BOC > ∠AOC,若∠AOB = $75^{\circ}$,则∠AOC =
25°
;(2)如图(2),已知∠AOB = $90^{\circ}$,若 OC,OD 是∠AOB 的两条三分线.
① 求∠COD 的度数;
② 在①的基础上,现以 O 为中心,将∠COD 顺时针旋转 $n^{\circ}$得到∠C'OD'. 当 OA 恰好是∠C'OD'的三分线时,求 n 的值.
(1)(2)

(2)①30°;②n=40°或 50°.
答案:(1)25°;(2)①30°;②n=40°或 50°.