19. (10 分)按要求解答:
(1)如图,① 画直线 AB;
② 画射线 CD;
③ 连接 AD,BC 相交于点 P;
④ 连接 BD 并延长至点 Q,使 DQ = BD;
(2)已知一个角的补角比这个角的余角的 3 倍少 $50^{\circ}$,求这个角是多少度?
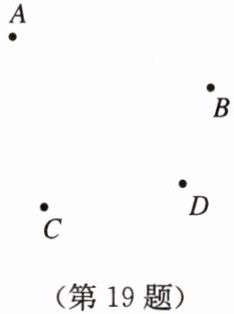
(1)如图,① 画直线 AB;
② 画射线 CD;
③ 连接 AD,BC 相交于点 P;
④ 连接 BD 并延长至点 Q,使 DQ = BD;
(2)已知一个角的补角比这个角的余角的 3 倍少 $50^{\circ}$,求这个角是多少度?

答案:
(1)如图所示: (2)这个角是 20 度.
(2)这个角是 20 度.
(1)如图所示:
 (2)这个角是 20 度.
(2)这个角是 20 度.20. (6 分)如图,∠AOB = $90^{\circ}$,∠COD = $90^{\circ}$,OE 平分∠BOD,∠DOE = $20^{\circ}$. 求∠AOC 的度数. 请将以下解答过程补充完整.
解:∵OE 平分∠BOD,
∴∠BOD = 2∠DOE(理由:
∵∠DOE = $20^{\circ}$,
∴∠BOD =
∵∠AOB = $90^{\circ}$,
∴∠BOC + ∠AOC = $90^{\circ}$.
∵∠COD = $90^{\circ}$,
∴∠BOC + ∠BOD = $90^{\circ}$.
∴∠AOC = ∠
∴∠AOC =

解:∵OE 平分∠BOD,
∴∠BOD = 2∠DOE(理由:
角平分线的定义
)∵∠DOE = $20^{\circ}$,
∴∠BOD =
40
°.∵∠AOB = $90^{\circ}$,
∴∠BOC + ∠AOC = $90^{\circ}$.
∵∠COD = $90^{\circ}$,
∴∠BOC + ∠BOD = $90^{\circ}$.
∴∠AOC = ∠
BOD
(理由:同角的余角相等
)∴∠AOC =
40
°.
答案:角平分线的定义;40;BOD;同角的余角相等;40
解析:
解:
∵OE 平分∠BOD,
∴∠BOD = 2∠DOE(理由:角平分线的定义)
∵∠DOE = $20^{\circ}$,
∴∠BOD = $40^{\circ}$.
∵∠AOB = $90^{\circ}$,
∴∠BOC + ∠AOC = $90^{\circ}$.
∵∠COD = $90^{\circ}$,
∴∠BOC + ∠BOD = $90^{\circ}$.
∴∠AOC = ∠BOD(理由:同角的余角相等)
∴∠AOC = $40^{\circ}$.
∵OE 平分∠BOD,
∴∠BOD = 2∠DOE(理由:角平分线的定义)
∵∠DOE = $20^{\circ}$,
∴∠BOD = $40^{\circ}$.
∵∠AOB = $90^{\circ}$,
∴∠BOC + ∠AOC = $90^{\circ}$.
∵∠COD = $90^{\circ}$,
∴∠BOC + ∠BOD = $90^{\circ}$.
∴∠AOC = ∠BOD(理由:同角的余角相等)
∴∠AOC = $40^{\circ}$.
21. (6 分)如图,已知轮船 A 在灯塔 P 的北偏东 $30^{\circ}$的方向,轮船 B 在灯塔 P 的南偏东 $70^{\circ}$的方向.
(1)从灯塔 P 看两轮船的视角(即∠APB)的度数是多少?
(2)轮船 C 在∠APB 的平分线上,则轮船 C 在灯塔 P 的什么方位?

(1)从灯塔 P 看两轮船的视角(即∠APB)的度数是多少?
(2)轮船 C 在∠APB 的平分线上,则轮船 C 在灯塔 P 的什么方位?

答案:(1)80°. (2)轮船 C 在灯塔 P 的北偏东70°的方向上.
解析:
(1)由题意得,轮船A在灯塔P的北偏东$30^{\circ}$方向,轮船B在灯塔P的南偏东$70^{\circ}$方向。
因为正北方向与正南方向夹角为$180^{\circ}$,所以$\angle APB=180^{\circ}-30^{\circ}-70^{\circ}=80^{\circ}$。
(2)因为PC是$\angle APB$的平分线,$\angle APB = 80^{\circ}$,所以$\angle APC=\frac{1}{2}\angle APB=\frac{1}{2}×80^{\circ}=40^{\circ}$。
又因为轮船A在灯塔P的北偏东$30^{\circ}$方向,所以轮船C在灯塔P的北偏东$30^{\circ}+40^{\circ}=70^{\circ}$方向。
因为正北方向与正南方向夹角为$180^{\circ}$,所以$\angle APB=180^{\circ}-30^{\circ}-70^{\circ}=80^{\circ}$。
(2)因为PC是$\angle APB$的平分线,$\angle APB = 80^{\circ}$,所以$\angle APC=\frac{1}{2}\angle APB=\frac{1}{2}×80^{\circ}=40^{\circ}$。
又因为轮船A在灯塔P的北偏东$30^{\circ}$方向,所以轮船C在灯塔P的北偏东$30^{\circ}+40^{\circ}=70^{\circ}$方向。
22. (8 分)如图,O 是直线 AB 上的一点,∠COD = $90^{\circ}$.
(1)若∠BOD = $32^{\circ}$,求∠AOC 的度数.
(2)若∠AOC : ∠BOD = 2 : 1,直接写出∠BOD 的度数.

(1)若∠BOD = $32^{\circ}$,求∠AOC 的度数.
(2)若∠AOC : ∠BOD = 2 : 1,直接写出∠BOD 的度数.

答案:(1)58°. (2)30°.
解析:
(1)因为O是直线AB上的一点,所以∠AOB=180°。
又因为∠COD=90°,∠BOD=32°,
所以∠AOC=∠AOB - ∠COD - ∠BOD=180° - 90° - 32°=58°。
(2)设∠BOD=x,则∠AOC=2x。
因为∠AOB=180°,∠COD=90°,
所以∠AOC + ∠COD + ∠BOD=180°,
即2x + 90° + x=180°,
3x=90°,
x=30°,
所以∠BOD=30°。
又因为∠COD=90°,∠BOD=32°,
所以∠AOC=∠AOB - ∠COD - ∠BOD=180° - 90° - 32°=58°。
(2)设∠BOD=x,则∠AOC=2x。
因为∠AOB=180°,∠COD=90°,
所以∠AOC + ∠COD + ∠BOD=180°,
即2x + 90° + x=180°,
3x=90°,
x=30°,
所以∠BOD=30°。