7. 若∠1,∠2 互为余角,且∠1 > ∠2,则∠2 的补角是(
A.2(∠1 - ∠2)
B.2(∠1 + ∠2)
C.2∠1 + ∠2
D.∠1 + 2∠2
C
)A.2(∠1 - ∠2)
B.2(∠1 + ∠2)
C.2∠1 + ∠2
D.∠1 + 2∠2
答案:C
解析:
∵∠1,∠2互为余角,
∴∠1+∠2=90°,
∠2的补角=180°-∠2,
∵∠1+∠2=90°,
∴180°=2(∠1+∠2),
∴∠2的补角=2(∠1+∠2)-∠2=2∠1+2∠2-∠2=2∠1+∠2,
C
8. 在直线 m 上顺次取 A,B,C 三点,使 AB = 10 cm,BC = 4 cm,如果点 O 是线段 AC 的中点,则线段 OB 的长为(
A.3 cm
B.7 cm
C.3 cm 或 7 cm
D.5 cm 或 2 cm
A
)A.3 cm
B.7 cm
C.3 cm 或 7 cm
D.5 cm 或 2 cm
答案:A
解析:
∵A,B,C在直线m上顺次排列,AB=10 cm,BC=4 cm,
∴AC=AB+BC=10+4=14 cm.
∵点O是线段AC的中点,
∴AO=AC/2=14/2=7 cm.
∴OB=AB-AO=10-7=3 cm.
A
9. $46^{\circ}35'$的余角等于
43°25′
.答案:43°25′
解析:
$90^{\circ}-46^{\circ}35'=43^{\circ}25'$
10. 如图,OA 是北偏东 $21^{\circ}48'$方向的一条射线,若∠BOA = $90^{\circ}$,则仿照表示 OA 方向的方法表示射线 OB 的方向:
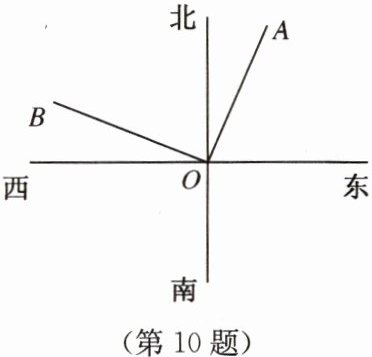
北偏西 68°12′
.
答案:北偏西 68°12′
解析:
北偏西 $68°12'$
11. 弯曲的公路改直后就能缩短路程,可以用数学知识的基本事实来解释为:
两点之间,线段最短
.答案:两点之间,线段最短
12. 已知α,β都是钝角,甲、乙、丙、丁四人计算$\frac{1}{6}$(α + β)的结果依次是 $28^{\circ}$, $48^{\circ}$, $60^{\circ}$, $88^{\circ}$,其中只有一人计算正确,他是
乙
.答案:乙
解析:
因为α,β都是钝角,所以$90^{\circ} < \alpha < 180^{\circ}$,$90^{\circ} < \beta < 180^{\circ}$。
则$90^{\circ} + 90^{\circ} < \alpha + \beta < 180^{\circ} + 180^{\circ}$,即$180^{\circ} < \alpha + \beta < 360^{\circ}$。
两边同时除以6,得$\frac{180^{\circ}}{6} < \frac{1}{6}(\alpha + \beta) < \frac{360^{\circ}}{6}$,即$30^{\circ} < \frac{1}{6}(\alpha + \beta) < 60^{\circ}$。
在$28^{\circ}$,$48^{\circ}$,$60^{\circ}$,$88^{\circ}$中,只有$48^{\circ}$满足$30^{\circ} < 48^{\circ} < 60^{\circ}$。
乙
则$90^{\circ} + 90^{\circ} < \alpha + \beta < 180^{\circ} + 180^{\circ}$,即$180^{\circ} < \alpha + \beta < 360^{\circ}$。
两边同时除以6,得$\frac{180^{\circ}}{6} < \frac{1}{6}(\alpha + \beta) < \frac{360^{\circ}}{6}$,即$30^{\circ} < \frac{1}{6}(\alpha + \beta) < 60^{\circ}$。
在$28^{\circ}$,$48^{\circ}$,$60^{\circ}$,$88^{\circ}$中,只有$48^{\circ}$满足$30^{\circ} < 48^{\circ} < 60^{\circ}$。
乙
13. 如图,D 是 BC 的中点,AB = 10,AC = 2,则 AD =

6
.
答案:6
解析:
∵D是BC的中点,
∴CD=BD。
由图可知,AC=2,AB=10,
∴BC=AB - AC=10 - 2=8,
∴CD=$\frac{1}{2}$BC=$\frac{1}{2}×8$=4,
∴AD=AC + CD=2 + 4=6。
6
14. 如图所示是正方体的一种展开图,表面上的语句为北京 2022 年冬奥会和冬残奥会的主题口号“一起向未来!”,那么在正方体的表面与“向”相对的汉字是

来
.
答案:来
15. 如图,∠AOB = $20^{\circ}$,∠AOC = $90^{\circ}$,点 B,O,D 在同一条直线上,那么∠COD = ______.


110°
答案:110°
解析:
∵∠AOB=20°,点B,O,D在同一条直线上,
∴∠AOD=180°-∠AOB=180°-20°=160°.
∵∠AOC=90°,
∴∠COD=∠AOD-∠AOC=160°-90°=70°.
70°
16. 某天,王同学午餐后,从中午 12 点开始到 13 点之间在教室阅读,读完后,他看到教室里挂钟的时针与分针的夹角为 $140^{\circ}$,则他今天阅读了
40 或 $\frac{280}{11}$
分钟.答案:40 或 $\frac{280}{11}$
解析:
设王同学阅读了$x$分钟,12点时,时针与分针重合,夹角为$0^{\circ}$。
分针每分钟转$6^{\circ}$,$x$分钟转$6x^{\circ}$;时针每分钟转$0.5^{\circ}$,$x$分钟转$0.5x^{\circ}$。
情况一:分针在时针前方,夹角为$140^{\circ}$,则$6x - 0.5x = 140$,解得$x = \frac{280}{11}$。
情况二:分针在时针后方,夹角为$140^{\circ}$,则$6x - 0.5x = 360 - 140$,解得$x = 40$。
$\frac{280}{11}$和$40$均在$0$到$60$之间,符合题意。
40或$\frac{280}{11}$
分针每分钟转$6^{\circ}$,$x$分钟转$6x^{\circ}$;时针每分钟转$0.5^{\circ}$,$x$分钟转$0.5x^{\circ}$。
情况一:分针在时针前方,夹角为$140^{\circ}$,则$6x - 0.5x = 140$,解得$x = \frac{280}{11}$。
情况二:分针在时针后方,夹角为$140^{\circ}$,则$6x - 0.5x = 360 - 140$,解得$x = 40$。
$\frac{280}{11}$和$40$均在$0$到$60$之间,符合题意。
40或$\frac{280}{11}$
17. 如图,在正方形网格中,点 O,A,B,C,D 均是格点. 若 OE 平分∠BOC,则∠DOE 的度数为

22.5
°.
答案:22.5
解析:
由图可知,∠BOC=135°,OE平分∠BOC,所以∠BOE=∠COE=67.5°。∠BOD=90°,则∠DOE=∠BOD - ∠BOE=90° - 67.5°=22.5°
22.5
22.5
18. 如图,在长方形 ABCD 中,点 E 在 AD 上,且∠AEB = $65^{\circ}$,分别以 BE,CE 为折痕进行折叠并压平,若∠A'ED' = $10^{\circ}$,则∠DEC 的度数为

30°
.
答案:30°
解析:
设∠DEC = x。
由折叠性质得:∠AEB = ∠A'EB = 65°,∠DEC = ∠D'EC = x。
∵∠AEB + ∠A'EB + ∠A'ED' + ∠D'EC + ∠DEC = 180°,∠A'ED' = 10°,
∴65° + 65° + 10° + x + x = 180°。
解得x = 20°。
20°
由折叠性质得:∠AEB = ∠A'EB = 65°,∠DEC = ∠D'EC = x。
∵∠AEB + ∠A'EB + ∠A'ED' + ∠D'EC + ∠DEC = 180°,∠A'ED' = 10°,
∴65° + 65° + 10° + x + x = 180°。
解得x = 20°。
20°