1. 下列说法正确的是(
A.直线 AB 与直线 BA 不是同一条直线
B.射线 AB 与射线 BA 是同一条射线
C.延长线段 AB 和延长线段 BA 的含义一样
D.线段 AB 与线段 BA 是同一条线段
D
)A.直线 AB 与直线 BA 不是同一条直线
B.射线 AB 与射线 BA 是同一条射线
C.延长线段 AB 和延长线段 BA 的含义一样
D.线段 AB 与线段 BA 是同一条线段
答案:D
2. 如图,从物体上面看到的平面图形是(


C
)

答案:C
3. 如图,将甲、乙两把尺子拼在一起,两端重合,如果甲尺经校定是直的,那么乙尺不是直的,判断依据是(

A.两点之间直线最短
B.经过一点有且只有一条直线
C.经过两点有且只有一条直线
D.线段可以向两个方向延长
C
)
A.两点之间直线最短
B.经过一点有且只有一条直线
C.经过两点有且只有一条直线
D.线段可以向两个方向延长
答案:C
4. 下列说法正确的有(
① 角的大小与所画边的长短无关;
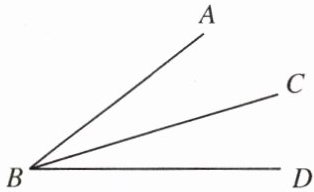
② 如图,∠ABD 也可用∠B 表示;
③ 如果∠AOC = $\frac{1}{2}$∠AOB,那么 OC 是∠AOB 的平分线;
④ 连接两点的线段叫作这两点之间的距离;
⑤ 两点之间线段最短;
⑥ 点 E 在线段 CD 上,若 DE = $\frac{1}{2}$CD,则点 E 是线段 CD 的中点.
A.1 个
B.2 个
C.3 个
D.4 个
C
)① 角的大小与所画边的长短无关;
② 如图,∠ABD 也可用∠B 表示;
③ 如果∠AOC = $\frac{1}{2}$∠AOB,那么 OC 是∠AOB 的平分线;
④ 连接两点的线段叫作这两点之间的距离;
⑤ 两点之间线段最短;
⑥ 点 E 在线段 CD 上,若 DE = $\frac{1}{2}$CD,则点 E 是线段 CD 的中点.

A.1 个
B.2 个
C.3 个
D.4 个
答案:C
解析:
①角的大小与所画边的长短无关,正确;
②图中以点B为顶点的角不止一个,∠ABD不可用∠B表示,错误;
③若∠AOC=$\frac{1}{2}$∠AOB,当OC不在∠AOB内部时,OC不是∠AOB的平分线,错误;
④连接两点的线段的长度叫作这两点之间的距离,错误;
⑤两点之间线段最短,正确;
⑥点E在线段CD上,DE=$\frac{1}{2}$CD,则CE=CD-DE=$\frac{1}{2}$CD,点E是线段CD的中点,正确。
正确的有①⑤⑥,共3个。
C
②图中以点B为顶点的角不止一个,∠ABD不可用∠B表示,错误;
③若∠AOC=$\frac{1}{2}$∠AOB,当OC不在∠AOB内部时,OC不是∠AOB的平分线,错误;
④连接两点的线段的长度叫作这两点之间的距离,错误;
⑤两点之间线段最短,正确;
⑥点E在线段CD上,DE=$\frac{1}{2}$CD,则CE=CD-DE=$\frac{1}{2}$CD,点E是线段CD的中点,正确。
正确的有①⑤⑥,共3个。
C
5. A 看 B 的方向是北偏东 $30^{\circ}$,那么 B 看 A 的方向是(
A.南偏东 $60^{\circ}$
B.南偏西 $60^{\circ}$
C.南偏东 $30^{\circ}$
D.南偏西 $30^{\circ}$
D
)A.南偏东 $60^{\circ}$
B.南偏西 $60^{\circ}$
C.南偏东 $30^{\circ}$
D.南偏西 $30^{\circ}$
答案:D
6. 如图,数轴上点 A 和点 B 表示的数分别是 -1 和 3,点 P 到 A,B 两点的距离之和为 6,则点 P 表示的数是(

A.-3
B.-3 或 5
C.-2
D.-2 或 4
D
)
A.-3
B.-3 或 5
C.-2
D.-2 或 4
答案:D
解析:
设点P表示的数是$x$。
点A表示的数是$-1$,点B表示的数是$3$,则$PA = |x - (-1)| = |x + 1|$,$PB = |x - 3|$。
已知$PA + PB = 6$,即$|x + 1| + |x - 3| = 6$。
当$x < -1$时,$x + 1 < 0$,$x - 3 < 0$,方程化为$-(x + 1) - (x - 3) = 6$,解得$x = -2$。
当$-1 \leq x \leq 3$时,$x + 1 \geq 0$,$x - 3 \leq 0$,方程化为$(x + 1) - (x - 3) = 6$,即$4 = 6$,无解。
当$x > 3$时,$x + 1 > 0$,$x - 3 > 0$,方程化为$(x + 1) + (x - 3) = 6$,解得$x = 4$。
综上,点P表示的数是$-2$或$4$。
D
点A表示的数是$-1$,点B表示的数是$3$,则$PA = |x - (-1)| = |x + 1|$,$PB = |x - 3|$。
已知$PA + PB = 6$,即$|x + 1| + |x - 3| = 6$。
当$x < -1$时,$x + 1 < 0$,$x - 3 < 0$,方程化为$-(x + 1) - (x - 3) = 6$,解得$x = -2$。
当$-1 \leq x \leq 3$时,$x + 1 \geq 0$,$x - 3 \leq 0$,方程化为$(x + 1) - (x - 3) = 6$,即$4 = 6$,无解。
当$x > 3$时,$x + 1 > 0$,$x - 3 > 0$,方程化为$(x + 1) + (x - 3) = 6$,解得$x = 4$。
综上,点P表示的数是$-2$或$4$。
D