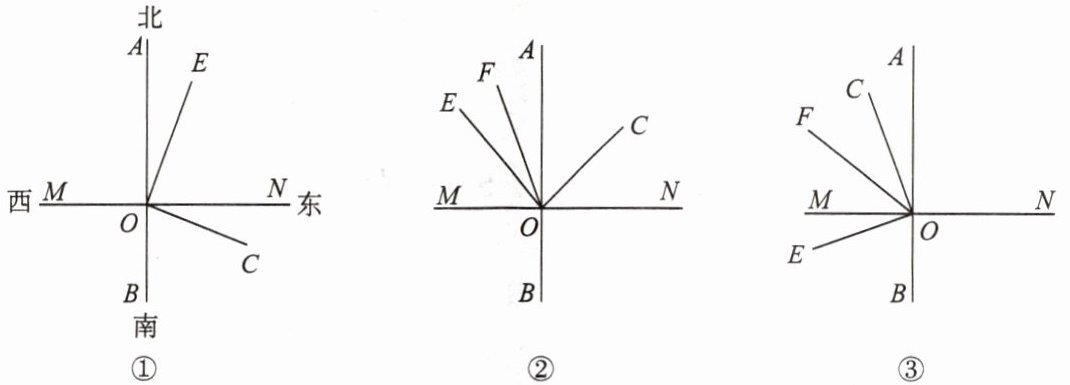
已知：$O为直线AB$上的一点,以$O$为观察中心,射线$OA$表示正北方向,$ON$表示正东方向(即$AB \perp MN$),射线$OC$、射线$OE$的方向如各图所示。
(1)如图①,当$\angle COE = 90^{\circ}$时：
① 若$\angle AOE = 20^{\circ}$,则射线$OE$的方向是。
② $\angle AOE与\angle CON$的关系为。
③ $\angle AOC与\angle EON$的关系为。
(2)若将射线$OC$、射线$OE绕点O$旋转至图②的位置,另一条射线$OF恰好平分\angle COM$,旋转过程中始终保持$\angle COE = 90^{\circ}$。
① 若$\angle AOF = 24^{\circ}$,则$\angle EOF = $度。
② 若$\angle AOF = \beta$,则$\angle CON = $(用含$\beta$的代数式表示)。
(3)若将射线$OC$、射线$OE绕点O$旋转至图③的位置,射线$OF仍然平分\angle COM$,旋转过程中始终保持$\angle COE = 90^{\circ}$,则$\angle CON与\angle AOF$之间存在怎样的数量关系？说明理由。