10. 若代数式 $y^{2} + 2y + 7$ 的值为 $6$,则代数式 $4y^{2} + 8y - 5$ 的值为(
A.$-9$
B.$9$
C.$18$
D.$-18$
A
)A.$-9$
B.$9$
C.$18$
D.$-18$
答案:A
解析:
由题意得:$y^{2} + 2y + 7 = 6$,则$y^{2} + 2y = 6 - 7 = -1$。
$4y^{2} + 8y - 5 = 4(y^{2} + 2y) - 5$,将$y^{2} + 2y = -1$代入得:
$4×(-1) - 5 = -4 - 5 = -9$
A
$4y^{2} + 8y - 5 = 4(y^{2} + 2y) - 5$,将$y^{2} + 2y = -1$代入得:
$4×(-1) - 5 = -4 - 5 = -9$
A
11. 如图所示是一个切去了一个角的正方体纸盒,切面与棱的交点 $A$,$B$,$C$ 均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是(
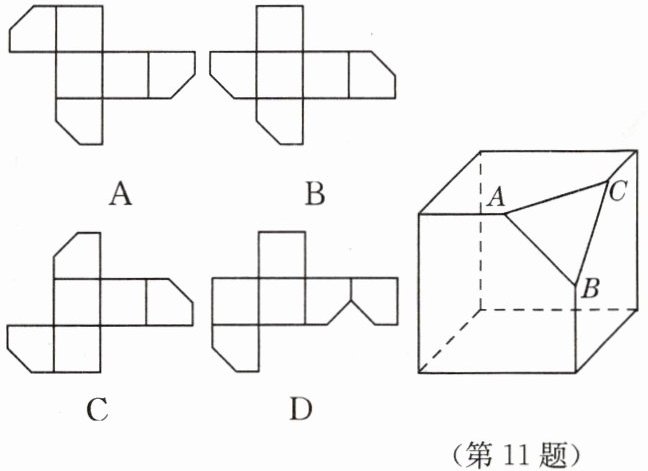
B
)
答案:B
12. 如图,点 $M$ 在线段 $AN$ 的延长线上,且线段 $MN = 20$,第一次操作:分别取线段 $AM$ 和 $AN$ 的中点 $M_{1}$,$N_{1}$.第二次操作:分别取线段 $AM_{1}$ 和 $AN_{1}$ 的中点 $M_{2}$,$N_{2}$.第三次操作:分别取线段 $AM_{2}$ 和 $AN_{2}$ 的中点 $M_{3}$,$N_{3}$……连续这样操作 $10$ 次,则 $M_{10}N_{10} = $(

A.$2$
B.$\dfrac{20}{2^{9}}$
C.$\dfrac{20}{2^{10}}$
D.$\dfrac{20}{2^{11}}$
C
)
A.$2$
B.$\dfrac{20}{2^{9}}$
C.$\dfrac{20}{2^{10}}$
D.$\dfrac{20}{2^{11}}$
答案:C
解析:
设线段$AN = x$,则$AM = AN + NM = x + 20$。
第一次操作:$M_1$为$AM$中点,$AM_1=\dfrac{AM}{2}=\dfrac{x + 20}{2}$;$N_1$为$AN$中点,$AN_1=\dfrac{AN}{2}=\dfrac{x}{2}$。$M_1N_1 = AM_1 - AN_1=\dfrac{x + 20}{2}-\dfrac{x}{2}=10=\dfrac{20}{2^1}$。
第二次操作:$M_2$为$AM_1$中点,$AM_2=\dfrac{AM_1}{2}=\dfrac{x + 20}{4}$;$N_2$为$AN_1$中点,$AN_2=\dfrac{AN_1}{2}=\dfrac{x}{4}$。$M_2N_2 = AM_2 - AN_2=\dfrac{x + 20}{4}-\dfrac{x}{4}=5=\dfrac{20}{2^2}$。
第三次操作:同理可得$M_3N_3=\dfrac{20}{2^3}$。
……
第$n$次操作:$M_nN_n=\dfrac{20}{2^n}$。
当$n = 10$时,$M_{10}N_{10}=\dfrac{20}{2^{10}}$。
C
第一次操作:$M_1$为$AM$中点,$AM_1=\dfrac{AM}{2}=\dfrac{x + 20}{2}$;$N_1$为$AN$中点,$AN_1=\dfrac{AN}{2}=\dfrac{x}{2}$。$M_1N_1 = AM_1 - AN_1=\dfrac{x + 20}{2}-\dfrac{x}{2}=10=\dfrac{20}{2^1}$。
第二次操作:$M_2$为$AM_1$中点,$AM_2=\dfrac{AM_1}{2}=\dfrac{x + 20}{4}$;$N_2$为$AN_1$中点,$AN_2=\dfrac{AN_1}{2}=\dfrac{x}{4}$。$M_2N_2 = AM_2 - AN_2=\dfrac{x + 20}{4}-\dfrac{x}{4}=5=\dfrac{20}{2^2}$。
第三次操作:同理可得$M_3N_3=\dfrac{20}{2^3}$。
……
第$n$次操作:$M_nN_n=\dfrac{20}{2^n}$。
当$n = 10$时,$M_{10}N_{10}=\dfrac{20}{2^{10}}$。
C
13. 计算:$-5 + 3 = $
-2
,$3x + 2(x - 2) = $5x - 4
.答案:-2;5x - 4
14. 利用隧道可把弯曲的公路改直,就能缩短两地的路程,这其中蕴含的数学道理是
两点之间线段最短
.答案:两点之间线段最短
15. 把 $54.965$ 精确到十分位是
55.0
.答案:55.0
16. 《孙子算经》中有一道题,原文是:今有四人共车,一车空;三人共车,九人步,问车有几何?译文为:今有若干人乘车,每 $4$ 人共乘一车,则剩余 $1$ 辆车无人乘坐;若每 $3$ 人共乘一车,则剩余 $9$ 个人无车可乘,问共有多少辆车?设共有 $x$ 辆车,则可列方程为
4(x - 1)=3x + 9
.答案:4(x - 1)=3x + 9
17. 一个角的补角是这个角余角的 $6$ 倍,则这个角的度数是
72°
.答案:72°
解析:
设这个角的度数为$x$。
由题意得:$180° - x = 6(90° - x)$
解得:$x = 72°$
$72°$
由题意得:$180° - x = 6(90° - x)$
解得:$x = 72°$
$72°$
18. 一个单项式含 $x$,$y$ 这两个字母,并且它的系数是 $-3$,次数是 $4$,试写出所有符合条件的单项式:
-3x³y,-3x²y²,-3xy³
.答案:-3x³y,-3x²y²,-3xy³
解析:
$-3x^{3}y,$$-3x^{2}y^{2},$$-3xy^{3}$
19. 如图,已知 $\angle AOB = \alpha$,$\angle BOC = \beta$,$OM$ 平分 $\angle AOC$,$ON$ 平分 $\angle BOC$,则 $\angle MON$ 的度数是

$\frac{1}{2}α$
.
答案:$\frac{1}{2}α$
解析:
$\angle AOC = \angle AOB + \angle BOC = \alpha + \beta$
$OM$平分$\angle AOC$,则$\angle MOC = \frac{1}{2}\angle AOC = \frac{1}{2}(\alpha + \beta)$
$ON$平分$\angle BOC$,则$\angle NOC = \frac{1}{2}\angle BOC = \frac{1}{2}\beta$
$\angle MON = \angle MOC - \angle NOC = \frac{1}{2}(\alpha + \beta) - \frac{1}{2}\beta = \frac{1}{2}\alpha$
$\frac{1}{2}\alpha$
$OM$平分$\angle AOC$,则$\angle MOC = \frac{1}{2}\angle AOC = \frac{1}{2}(\alpha + \beta)$
$ON$平分$\angle BOC$,则$\angle NOC = \frac{1}{2}\angle BOC = \frac{1}{2}\beta$
$\angle MON = \angle MOC - \angle NOC = \frac{1}{2}(\alpha + \beta) - \frac{1}{2}\beta = \frac{1}{2}\alpha$
$\frac{1}{2}\alpha$
20. 同一数轴上有点 $A$,$C$ 分别表示数 $a$,$c$,且 $a$,$c$ 满足等式 $(16 + a)^{2} + |c - 12| = 0$,点 $B$ 表示的数是多项式 $2x^{2} - 4x + 3$ 的一次项系数,点 $A$,$B$,$C$ 在数轴上同时开始运动,点 $A$ 向左运动,速度为每秒 $3$ 个单位长度,点 $B$,$C$ 均向右运动,速度分别为每秒 $3$ 个单位长度和每秒 $4$ 个单位长度,设运动时间为 $t$ 秒.若存在 $m$ 使得 $2AB - m\cdot BC$ 的值不随时间 $t$ 的变化而改变,则该定值为
-168
.答案:-168
解析:
因为$(16 + a)^{2} + |c - 12| = 0$,$(16 + a)^{2}\geq0$,$|c - 12|\geq0$,所以$16 + a = 0$,$c - 12 = 0$,解得$a=-16$,$c=12$,即点$A$表示$-16$,点$C$表示$12$。多项式$2x^{2}-4x + 3$的一次项系数为$-4$,所以点$B$表示$-4$。
运动$t$秒后,点$A$表示的数为$-16-3t$,点$B$表示的数为$-4 + 3t$,点$C$表示的数为$12+4t$。
$AB=(-4 + 3t)-(-16-3t)=12 + 6t$,$BC=(12 + 4t)-(-4 + 3t)=16 + t$。
$2AB - m\cdot BC=2(12 + 6t)-m(16 + t)=(12 - 16m)+(12 - m)t$。
因为$2AB - m\cdot BC$的值不随时间$t$变化,所以$12 - m=0$,解得$m=12$。此时$2AB - m\cdot BC=12-16×12=-168$。
$-168$
运动$t$秒后,点$A$表示的数为$-16-3t$,点$B$表示的数为$-4 + 3t$,点$C$表示的数为$12+4t$。
$AB=(-4 + 3t)-(-16-3t)=12 + 6t$,$BC=(12 + 4t)-(-4 + 3t)=16 + t$。
$2AB - m\cdot BC=2(12 + 6t)-m(16 + t)=(12 - 16m)+(12 - m)t$。
因为$2AB - m\cdot BC$的值不随时间$t$变化,所以$12 - m=0$,解得$m=12$。此时$2AB - m\cdot BC=12-16×12=-168$。
$-168$