28. (12 分)定义：若一个关于 $x$ 的方程 $ax + b = 0(a \neq 0)$ 的解为 $x = \dfrac{a + b}{2}$,则称此方程为“中点方程”.
例如：$x - \dfrac{1}{3} = 0$ 的解为 $x = \dfrac{1}{3}$,而 $\dfrac{1}{3} = \dfrac{1}{2}× (1 - \dfrac{1}{3})$；$2x - 1 = 0$ 的解为 $x = \dfrac{1}{2}$,而 $\dfrac{1}{2} = \dfrac{1}{2}× (2 - 1)$.
(1)判断方程：
① $3x + 1 = 0$；
② $x - 2 = 0$；
③ $-x - 1 = 0$.
其中是“中点方程”的是 ；
(2)若 $a = 2$ 且方程 $ax + b = 0$ 为“中点方程”,求 $3a - b$ 的值；

(3)若关于 $x$ 的方程 $2ax + b = bx$ 是“中点方程”,求代数式 $6a^{2} - 3ab + 3b + 2025$ 的值.

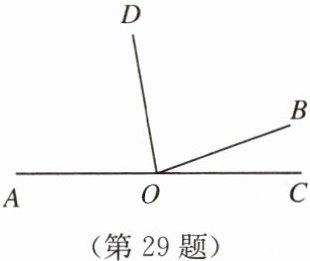
29. (12 分)已知点 $A$,$O$,$C$ 在同一条直线上,射线 $OB$ 在 $AC$ 上方,且 $\angle BOC = 20^{\circ}$.
(1)若射线 $OD$ 平分 $\angle AOB$,求 $\angle BOD$ 的度数；
(2)射线 $OM$ 以 $30^{\circ}$ 每秒的速度从射线 $OA$ 开始顺时针运动,$\angle POQ$ 开始时与 $\angle BOC$ 重合,其中 $OP$ 与 $OB$ 重合,以 $10^{\circ}$ 每秒的速度逆时针运动.
① 当运动时间为多长时,射线 $OM$ 和 $\angle POQ$ 的角平分线重合？
② 试探究是否存在运动到某一时刻,$\angle MOP = \dfrac{1}{2}\angle MOQ$.若存在,求出所有符合条件的 $\angle AOM$ 的度数；若不存在,请说明理由.