25. (8 分)玲玲做一道题“已知两个多项式 $A$,$B$,其中 $A = x^{2} + 3x - 5$,计算 $A - 2B$”,她误将“$A - 2B$”写成“$2A - B$”,结果答案是 $x^{2} + 8x - 7$,你能帮助她求出正确答案吗?
答案:先求出 B = x² - 2x - 3,从而 A - 2B = -x² + 7x + 1
解析:
因为$2A - B = x^{2} + 8x - 7$,且$A = x^{2} + 3x - 5$,所以$B = 2A - (x^{2} + 8x - 7)$。
$B = 2(x^{2} + 3x - 5) - (x^{2} + 8x - 7)$
$= 2x^{2} + 6x - 10 - x^{2} - 8x + 7$
$= (2x^{2} - x^{2}) + (6x - 8x) + (-10 + 7)$
$= x^{2} - 2x - 3$
则$A - 2B = (x^{2} + 3x - 5) - 2(x^{2} - 2x - 3)$
$= x^{2} + 3x - 5 - 2x^{2} + 4x + 6$
$= (x^{2} - 2x^{2}) + (3x + 4x) + (-5 + 6)$
$= -x^{2} + 7x + 1$
正确答案是$-x^{2} + 7x + 1$。
$B = 2(x^{2} + 3x - 5) - (x^{2} + 8x - 7)$
$= 2x^{2} + 6x - 10 - x^{2} - 8x + 7$
$= (2x^{2} - x^{2}) + (6x - 8x) + (-10 + 7)$
$= x^{2} - 2x - 3$
则$A - 2B = (x^{2} + 3x - 5) - 2(x^{2} - 2x - 3)$
$= x^{2} + 3x - 5 - 2x^{2} + 4x + 6$
$= (x^{2} - 2x^{2}) + (3x + 4x) + (-5 + 6)$
$= -x^{2} + 7x + 1$
正确答案是$-x^{2} + 7x + 1$。
26. (12 分)如图(1),点 $B$,$C$ 在线段 $AD$ 上.
(1)图中共有
(2)比较线段的长短:若 $AB = CD$,则 $AC$
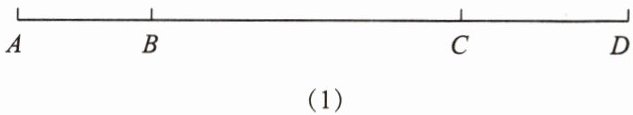
(3)如图(2),点 $B$,$C$ 在线段 $AD$ 上,点 $M$ 是 $AB$ 的中点,点 $N$ 是 $CD$ 的中点.
① 若 $AD = 20$,$BC = 12$,求 $MN$ 的长度;
② 若 $AD = a$,$BC = b$,求 $MN$ 的长度(用含有 $a$,$b$ 的代数式表示).

(1)图中共有
6
条线段;(2)比较线段的长短:若 $AB = CD$,则 $AC$
=
$BD$;(填:“$>$”“$<$”或“$=$”)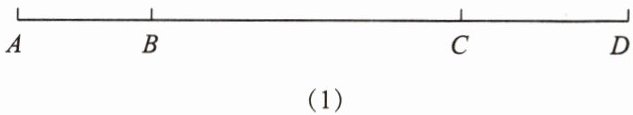
(3)如图(2),点 $B$,$C$ 在线段 $AD$ 上,点 $M$ 是 $AB$ 的中点,点 $N$ 是 $CD$ 的中点.
① 若 $AD = 20$,$BC = 12$,求 $MN$ 的长度;
② 若 $AD = a$,$BC = b$,求 $MN$ 的长度(用含有 $a$,$b$ 的代数式表示).

答案:解:
(1) 6.
(2) =.
(3) ①
∵AD = 20,BC = 12,
∴AB + CD = AD - BC = 20 - 12 = 8.
∵点 M 是 AB 的中点,点 N 是 CD 的中点,
∴BM = $\frac{1}{2}$AB,CN = $\frac{1}{2}$CD.
∵BC = 12,
∴MN = BC + BM + CN = BC + $\frac{1}{2}$AB + $\frac{1}{2}$CD = BC + $\frac{1}{2}$(AB + CD) = 12 + $\frac{1}{2}$×8 = 12 + 4 = 16. ②
∵AD = a,BC = b,
∴AB + CD = AD - BC = a - b. 由①可得 MN = BC + $\frac{1}{2}$(AB + CD),
∴MN = b + $\frac{1}{2}$(a - b) = $\frac{1}{2}$(a + b)
(1) 6.
(2) =.
(3) ①
∵AD = 20,BC = 12,
∴AB + CD = AD - BC = 20 - 12 = 8.
∵点 M 是 AB 的中点,点 N 是 CD 的中点,
∴BM = $\frac{1}{2}$AB,CN = $\frac{1}{2}$CD.
∵BC = 12,
∴MN = BC + BM + CN = BC + $\frac{1}{2}$AB + $\frac{1}{2}$CD = BC + $\frac{1}{2}$(AB + CD) = 12 + $\frac{1}{2}$×8 = 12 + 4 = 16. ②
∵AD = a,BC = b,
∴AB + CD = AD - BC = a - b. 由①可得 MN = BC + $\frac{1}{2}$(AB + CD),
∴MN = b + $\frac{1}{2}$(a - b) = $\frac{1}{2}$(a + b)
27. (12 分)已知点 $O$ 为直线 $AB$ 上一点,将直角三角板 $MON$ 的直角顶点放在点 $O$ 处,并在 $\angle MON$ 内部作射线 $OC$.
(1)将三角板放置到如图所示位置,使 $OC$ 恰好平分 $\angle MOB$,且 $\angle BON = 2\angle NOC$,求 $\angle AOM$ 的度数;
(2)若仍将三角板按照如图所示的方式放置,仅满足 $OC$ 平分 $\angle MOB$,试猜想 $\angle AOM$ 与 $\angle NOC$ 之间的数量关系,并说明理由.

(1)将三角板放置到如图所示位置,使 $OC$ 恰好平分 $\angle MOB$,且 $\angle BON = 2\angle NOC$,求 $\angle AOM$ 的度数;
(2)若仍将三角板按照如图所示的方式放置,仅满足 $OC$ 平分 $\angle MOB$,试猜想 $\angle AOM$ 与 $\angle NOC$ 之间的数量关系,并说明理由.

答案:
(1) ∠AOM = 45°;
(2) ∠AOM = 2∠NOC. 令∠NOC 为α,∠AOM 为β,则∠MOC = 90° - α.
∵∠AOM + ∠MOC + ∠BOC = 180°,
∴β + 90° - α + 90° - α = 180°,
∴β - 2α = 0,即β = 2α,
∴∠AOM = 2∠NOC
(1) ∠AOM = 45°;
(2) ∠AOM = 2∠NOC. 令∠NOC 为α,∠AOM 为β,则∠MOC = 90° - α.
∵∠AOM + ∠MOC + ∠BOC = 180°,
∴β + 90° - α + 90° - α = 180°,
∴β - 2α = 0,即β = 2α,
∴∠AOM = 2∠NOC