1. 已知$x$,$y$互为相反数,$a$,$b$互为倒数,$c$的绝对值为3,则$x + y + ab + \vert c\vert$的值是
4
.答案:4
解析:
因为$x$,$y$互为相反数,所以$x + y=0$;
因为$a$,$b$互为倒数,所以$ab = 1$;
因为$c$的绝对值为$3$,所以$\vert c\vert=3$。
则$x + y + ab+\vert c\vert=0 + 1+3=4$。
4
因为$a$,$b$互为倒数,所以$ab = 1$;
因为$c$的绝对值为$3$,所以$\vert c\vert=3$。
则$x + y + ab+\vert c\vert=0 + 1+3=4$。
4
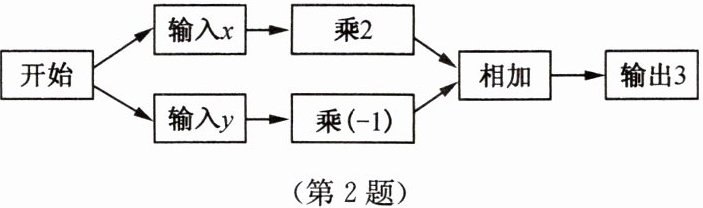
2. 按如图所示的运算程序,能使输出结果为3的是(
A.$x = 5$,$y = -2$
B.$x = 3$,$y = -2$
C.$x = -4$,$y = 2$
D.$x = -3$,$y = -9$
D
)
A.$x = 5$,$y = -2$
B.$x = 3$,$y = -2$
C.$x = -4$,$y = 2$
D.$x = -3$,$y = -9$
答案:D
解析:
由运算程序得:$2x + (-1)y = 3$,即$2x - y = 3$。
A. $x = 5$,$y = -2$时,$2×5 - (-2) = 12 ≠ 3$;
B. $x = 3$,$y = -2$时,$2×3 - (-2) = 8 ≠ 3$;
C. $x = -4$,$y = 2$时,$2×(-4) - 2 = -10 ≠ 3$;
D. $x = -3$,$y = -9$时,$2×(-3) - (-9) = 3$。
D
A. $x = 5$,$y = -2$时,$2×5 - (-2) = 12 ≠ 3$;
B. $x = 3$,$y = -2$时,$2×3 - (-2) = 8 ≠ 3$;
C. $x = -4$,$y = 2$时,$2×(-4) - 2 = -10 ≠ 3$;
D. $x = -3$,$y = -9$时,$2×(-3) - (-9) = 3$。
D
3. 对于算式$2026×(-8)+(-2026)×(-18)$,逆用分配律写成积的形式是(
A.$2026×(-8 - 18)$
B.$-2026×(-8 - 18)$
C.$2026×(-8 + 18)$
D.$-2026×(-8 + 18)$
C
)A.$2026×(-8 - 18)$
B.$-2026×(-8 - 18)$
C.$2026×(-8 + 18)$
D.$-2026×(-8 + 18)$
答案:C
解析:
$2026×(-8)+(-2026)×(-18)$
$=2026×(-8)+2026×18$
$=2026×(-8 + 18)$
C
$=2026×(-8)+2026×18$
$=2026×(-8 + 18)$
C
4. 若$abc = 0$,则下列选项正确的是(
A.$a$,$b$,$c$没有一个为0
B.$a$,$b$,$c$只有一个为0
C.$a$,$b$,$c$至少有一个为0
D.$a$,$b$,$c$三个都为0
C
)A.$a$,$b$,$c$没有一个为0
B.$a$,$b$,$c$只有一个为0
C.$a$,$b$,$c$至少有一个为0
D.$a$,$b$,$c$三个都为0
答案:C
5. 计算:
(1) $(-\frac{5}{6})×(-2.4)×(+\frac{4}{5})$; (2) $-2×(-3)×(-4)$;
(3) $-11 + (-4)×(-3)$; (4) $-0.25×0.5×(-3\frac{1}{5})×4$.
(1) $(-\frac{5}{6})×(-2.4)×(+\frac{4}{5})$; (2) $-2×(-3)×(-4)$;
(3) $-11 + (-4)×(-3)$; (4) $-0.25×0.5×(-3\frac{1}{5})×4$.
答案:(1)$\frac{8}{5}$;(2)-24;(3)1;(4)$\frac{8}{5}$.
解析:
(1) $(-\frac{5}{6})×(-2.4)×(+\frac{4}{5})$
$=(-\frac{5}{6})×(-\frac{12}{5})×\frac{4}{5}$
$=2×\frac{4}{5}$
$=\frac{8}{5}$
(2) $-2×(-3)×(-4)$
$=6×(-4)$
$=-24$
(3) $-11 + (-4)×(-3)$
$=-11 + 12$
$=1$
(4) $-0.25×0.5×(-3\frac{1}{5})×4$
$=(-\frac{1}{4})×\frac{1}{2}×(-\frac{16}{5})×4$
$=(-\frac{1}{4}×4)×(\frac{1}{2}×(-\frac{16}{5}))$
$=(-1)×(-\frac{8}{5})$
$=\frac{8}{5}$
问题 某校体育器材室共有60个篮球.一天课外活动,有3个班级分别计划借篮球总数的$\frac{1}{2}$,$\frac{1}{3}和\frac{1}{4}$.请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?
解题示范 (学生在教师指导下,独立完成)
解:
]
解题示范 (学生在教师指导下,独立完成)
解:
]
答案:解:
三个班级计划借篮球数分别为:
$60 × \frac{1}{2} = 30$(个),
$60 × \frac{1}{3} = 20$(个),
$60 × \frac{1}{4} = 15$(个)。
总计划借篮球数:
$30 + 20 + 15 = 65$(个)。
实际篮球数为60个,
$65 - 60 = 5$(个)。
因此,篮球不够借,还缺5个。
三个班级计划借篮球数分别为:
$60 × \frac{1}{2} = 30$(个),
$60 × \frac{1}{3} = 20$(个),
$60 × \frac{1}{4} = 15$(个)。
总计划借篮球数:
$30 + 20 + 15 = 65$(个)。
实际篮球数为60个,
$65 - 60 = 5$(个)。
因此,篮球不够借,还缺5个。