1. 甲数比乙数的3倍大2,若甲数为$x$,则乙数为(
A.$3x - 2$
B.$3x + 2$
C.$\frac{x + 2}{3}$
D.$\frac{x - 2}{3}$
D
)A.$3x - 2$
B.$3x + 2$
C.$\frac{x + 2}{3}$
D.$\frac{x - 2}{3}$
答案:D
解析:
由题意得,甲数$x$比乙数的3倍大2,即$x = 3× 乙数 + 2$,移项可得$3× 乙数 = x - 2$,则乙数为$\frac{x - 2}{3}$。
D
D
2. 某地冬季一天的温差是$15^{\circ}C$,这天最低气温是$t^{\circ}C$,则最高气温可列式表示为(
A.$(15 - t)^{\circ}C$
B.$(t - 15)^{\circ}C$
C.$(t + 15)^{\circ}C$
D.$(t - 15)^{\circ}C$
C
)A.$(15 - t)^{\circ}C$
B.$(t - 15)^{\circ}C$
C.$(t + 15)^{\circ}C$
D.$(t - 15)^{\circ}C$
答案:C
解析:
最高气温 = 最低气温 + 温差,即最高气温为$(t + 15)^{\circ}C$。
C
C
3. 原产量为$n$kg,增产$20\%$之后的产量应为(
A.$(1 - 20\%)n$kg
B.$(1 + 20\%)n$kg
C.$(n + 20\%)$kg
D.$n×20\%$kg
B
)A.$(1 - 20\%)n$kg
B.$(1 + 20\%)n$kg
C.$(n + 20\%)$kg
D.$n×20\%$kg
答案:B
解析:
原产量为$n$kg,增产$20\%$,即增加的产量为$20\%n$kg,所以增产之后的产量为原产量加上增加的产量,即$n + 20\%n=(1 + 20\%)n$kg。
B
B
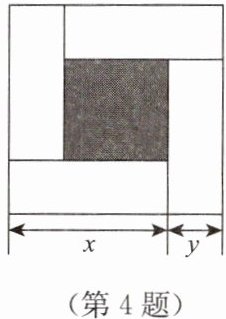
4. 如图,大正方形的边长为$m$,小正方形的边长为$n$,若用$x$,$y表示四个相同小长方形的两边长(x > y)$,给出以下关系式:①$x + y = m$;②$x - y = n$;③$xy = \frac{m^{2} - n^{2}}{4}$。其中正确的关系式的个数有(
A.0个
B.1个
C.2
D.3个
]
D
)
A.0个
B.1个
C.2
D.3个
]
答案:D
解析:
由图可知,大正方形边长为小长方形长与宽之和,即$x + y = m$,①正确;小正方形边长为小长方形长与宽之差,即$x - y = n$,②正确;大正方形面积减去小正方形面积为四个小长方形面积之和,$m^2 - n^2 = 4xy$,则$xy=\frac{m^2 - n^2}{4}$,③正确。正确的关系式有3个。
D
D
5. 用代数式表示:$a$的1.5倍与$y$的三分之一的差是
$\frac{3}{2}a-\frac{1}{3}y$
。答案:$\frac{3}{2}a-\frac{1}{3}y$
6. 对代数式$4a^{2}$作合理的解释:
4个边长为a的正方形的面积的和是$4a^{2}$(答案不唯一)
。答案:4个边长为a的正方形的面积的和是$4a^{2}$(答案不唯一)
解析:
边长为$2a$的正方形的面积是$4a^{2}$(答案不唯一)
7. 三个连续的偶数,中间的数是$a$,则$a$的前面和后面分别是
$a-2$
和$a+2$
。答案:$a-2$;$a+2$
8. 一个两位数,个位数字是$x$,十位数字比个位数字的2倍少3,这个两位数是
$21x-30$
。答案:$21x-30$
解析:
十位数字为$2x - 3$,这个两位数是$10(2x - 3) + x = 20x - 30 + x = 21x - 30$。
问题 根据题意列代数式:
(1)平行四边形高为$a$,底为$b$,求面积。
(2)一个两位数十位数字为$x$,个位数字为$y$,求这个数。
(3)某工程甲独做需$x$天,乙独做需$y$天,求两人合作需几天完成。
(4)甲、乙两数和的2倍为$n$,甲、乙两数之和为多少?
名师指导
(1)根据每个问题的数量关系列式。
(2)注意符合代数式的书写规范。
解题示范(学生在教师指导下,独立完成)
解:
]
(1)平行四边形高为$a$,底为$b$,求面积。
(2)一个两位数十位数字为$x$,个位数字为$y$,求这个数。
(3)某工程甲独做需$x$天,乙独做需$y$天,求两人合作需几天完成。
(4)甲、乙两数和的2倍为$n$,甲、乙两数之和为多少?
名师指导
(1)根据每个问题的数量关系列式。
(2)注意符合代数式的书写规范。
解题示范(学生在教师指导下,独立完成)
解:
]
答案:解:
(1) 面积 $S = a × b$,即 $S = ab$。
(2) 这个数可以表示为 $10x + y$。
(3) 甲工程每天完成 $\frac{1}{x}$,乙工程每天完成 $\frac{1}{y}$,两人合作每天完成 $\frac{1}{x} + \frac{1}{y}$,所以合作完成天数为 $1 ÷ \left( \frac{1}{x} + \frac{1}{y} \right) = \frac{xy}{x + y}$。
(4) 设甲、乙两数之和为 $M$,则 $2M = n$,所以 $M = \frac{n}{2}$。
(1) 面积 $S = a × b$,即 $S = ab$。
(2) 这个数可以表示为 $10x + y$。
(3) 甲工程每天完成 $\frac{1}{x}$,乙工程每天完成 $\frac{1}{y}$,两人合作每天完成 $\frac{1}{x} + \frac{1}{y}$,所以合作完成天数为 $1 ÷ \left( \frac{1}{x} + \frac{1}{y} \right) = \frac{xy}{x + y}$。
(4) 设甲、乙两数之和为 $M$,则 $2M = n$,所以 $M = \frac{n}{2}$。