1. 下列各式符合代数式书写规范的是(
A.$ b × 18 $
B.$ -\frac{b}{a^{2}} $
C.$ 1 \frac{1}{4} x $
D.$ m ÷ 2n $
B
)A.$ b × 18 $
B.$ -\frac{b}{a^{2}} $
C.$ 1 \frac{1}{4} x $
D.$ m ÷ 2n $
答案:B
2. 对于多项式 $ a^{2} + b^{2} $ 的意义解释不恰当的是(
A.$ a $,$ b $ 两数的平方和
B.边长分别是 $ a $,$ b $ 的两个正方形的面积和
C.买 $ a $ 支单价 $ a $ 元的钢笔和买 $ b $ 支单价 $ b $ 元的铅笔的总价钱
D.边长是 $ a + b $ 的正方形的面积
D
)A.$ a $,$ b $ 两数的平方和
B.边长分别是 $ a $,$ b $ 的两个正方形的面积和
C.买 $ a $ 支单价 $ a $ 元的钢笔和买 $ b $ 支单价 $ b $ 元的铅笔的总价钱
D.边长是 $ a + b $ 的正方形的面积
答案:D
3. “$ a $ 的 $ \frac{1}{2} $ 与 $ b $ 的 3 倍的差”用代数式表示是(
A.$ 3(\frac{1}{2} a - b) $
B.$ \frac{1}{2} a - 3b $
C.$ 3(a - \frac{1}{2} b) $
D.$ (a - \frac{1}{2}) - 3b $
B
)A.$ 3(\frac{1}{2} a - b) $
B.$ \frac{1}{2} a - 3b $
C.$ 3(a - \frac{1}{2} b) $
D.$ (a - \frac{1}{2}) - 3b $
答案:B
解析:
“$a$的$\frac{1}{2}$”表示为$\frac{1}{2}a$,“$b$的3倍”表示为$3b$,它们的差为$\frac{1}{2}a - 3b$。
B
B
4. 已知 $ m $ 是最大的负整数,$ a $,$ b $ 互为相反数,$ x $,$ y $ 互为倒数,则 $ m + (a + b) + xy $ 的值是(
A.$ -2 $
B.$ -1 $
C.$ 0 $
D.$ 1 $
C
)A.$ -2 $
B.$ -1 $
C.$ 0 $
D.$ 1 $
答案:C
解析:
因为$m$是最大的负整数,所以$m=-1$;
因为$a$,$b$互为相反数,所以$a + b=0$;
因为$x$,$y$互为倒数,所以$xy=1$;
则$m+(a + b)+xy=-1 + 0+1=0$。
C
因为$a$,$b$互为相反数,所以$a + b=0$;
因为$x$,$y$互为倒数,所以$xy=1$;
则$m+(a + b)+xy=-1 + 0+1=0$。
C
5. 2024 年苹果的价格比 2023 年上涨了 $ 10\% $,若 2024 年每千克苹果的价格是 $ a $ 元,则 2023 年每千克苹果的价格为(
A.$ (1 + 10\%) a $ 元
B.$ (1 - 10\%) a $ 元
C.$ \frac{a}{1 + 10\%} $ 元
D.$ \frac{a}{1 - 10\%} $ 元
C
)A.$ (1 + 10\%) a $ 元
B.$ (1 - 10\%) a $ 元
C.$ \frac{a}{1 + 10\%} $ 元
D.$ \frac{a}{1 - 10\%} $ 元
答案:C
解析:
设2023年每千克苹果的价格为$x$元。
2024年价格比2023年上涨$10\%$,则2024年价格为$x(1 + 10\%)$元。
已知2024年每千克苹果价格是$a$元,可得方程:$x(1 + 10\%)=a$。
解得:$x=\frac{a}{1 + 10\%}$。
C
2024年价格比2023年上涨$10\%$,则2024年价格为$x(1 + 10\%)$元。
已知2024年每千克苹果价格是$a$元,可得方程:$x(1 + 10\%)=a$。
解得:$x=\frac{a}{1 + 10\%}$。
C
6. 当 $ a = -2 $ 时,代数式 $ a(2a + 3) - 2a(a + 4) $ 的值是(
A.$ 10 $
B.$ -10 $
C.$ -8 $
D.$ 6 $
A
)A.$ 10 $
B.$ -10 $
C.$ -8 $
D.$ 6 $
答案:A
解析:
$a(2a + 3) - 2a(a + 4)$
$=2a^2 + 3a - 2a^2 - 8a$
$=-5a$
当$a = -2$时,原式$=-5×(-2)=10$
A
$=2a^2 + 3a - 2a^2 - 8a$
$=-5a$
当$a = -2$时,原式$=-5×(-2)=10$
A
7. 当 $ x = -1 $ 时,$ ax + b + 1 $ 的值为 $ -3 $,则 $ (a - b - 1)(1 - a + b) $ 的值为(
A.$ -9 $
B.$ 9 $
C.$ -25 $
D.$ 12 $
A
)A.$ -9 $
B.$ 9 $
C.$ -25 $
D.$ 12 $
答案:A
解析:
当$x = -1$时,$ax + b + 1=-3$,
即$a×(-1)+b + 1=-3$,
$-a + b + 1=-3$,
$-a + b=-4$,
$a - b=4$。
$(a - b - 1)(1 - a + b)=(a - b - 1)[-(a - b - 1)]$
$=-(a - b - 1)^{2}$
$=-(4 - 1)^{2}$
$=-9$
A
即$a×(-1)+b + 1=-3$,
$-a + b + 1=-3$,
$-a + b=-4$,
$a - b=4$。
$(a - b - 1)(1 - a + b)=(a - b - 1)[-(a - b - 1)]$
$=-(a - b - 1)^{2}$
$=-(4 - 1)^{2}$
$=-9$
A
8. 下面四个整式中,不能表示图中阴影部分面积的是(
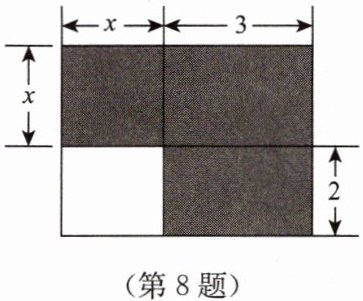
A.$ x^{2} + 5x $
B.$ x(x + 3) + 6 $
C.$ 3(x + 2) + x^{2} $
D.$ (x + 3)(x + 2) - 2x $
A
)
A.$ x^{2} + 5x $
B.$ x(x + 3) + 6 $
C.$ 3(x + 2) + x^{2} $
D.$ (x + 3)(x + 2) - 2x $
答案:A
9. 历史上,数学家欧拉最先把关于 $ x $ 的代数式用记号 $ f(x) $ 来表示,把 $ x $ 等于某数 $ a $ 的代数式的值用 $ f(a) $ 来表示. 例如 $ x = -2 $ 时,代数式 $ f(x) = -3x^{2} + x $ 的值记为 $ f(-2) $,那么 $ f(-2) $ 的值等于(
A.$ -10 $
B.$ -14 $
C.$ 10 $
D.$ 4 $
B
)A.$ -10 $
B.$ -14 $
C.$ 10 $
D.$ 4 $
答案:B
解析:
已知$f(x) = -3x^{2} + x$,则$f(-2)$为当$x=-2$时该代数式的值。
将$x=-2$代入$f(x)$可得:
$\begin{aligned}f(-2)&=-3×(-2)^{2}+(-2)\\&=-3×4 - 2\\&=-12 - 2\\&=-14\end{aligned}$
答案:B
将$x=-2$代入$f(x)$可得:
$\begin{aligned}f(-2)&=-3×(-2)^{2}+(-2)\\&=-3×4 - 2\\&=-12 - 2\\&=-14\end{aligned}$
答案:B
10. 如图是一种游戏,将正整数 1 至 2024 按一定规律排列如下. 通过按键操作平移或 $ 90^{\circ} $ 旋转图表中带阴影的方框,方框中三个数的和可能是(
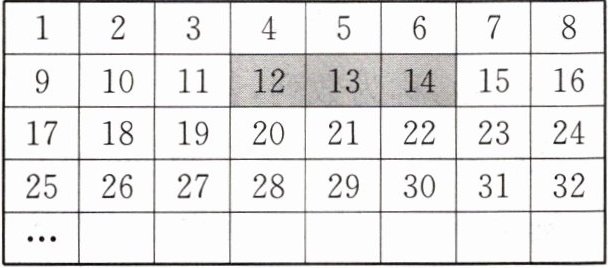
A.$ 2021 $
B.$ 2022 $
C.$ 2023 $
D.$ 2024 $
B
)
A.$ 2021 $
B.$ 2022 $
C.$ 2023 $
D.$ 2024 $
答案:B
解析:
情况1:水平方框(三个数在同一行)
设中间数为$x$,则三个数为$x-1$,$x$,$x+1$,和为$3x$,是3的倍数。
情况2:垂直方框(三个数在同一列)
每行8个数,设中间数为$x$,则三个数为$x-8$,$x$,$x+8$,和为$3x$,是3的倍数。
情况3:右倾对角线方框(左上-右下)
设中间数为$x$,则三个数为$x-9$,$x$,$x+9$,和为$3x$,是3的倍数。
情况4:左倾对角线方框(右上-左下)
设中间数为$x$,则三个数为$x-7$,$x$,$x+7$,和为$3x$,是3的倍数。
结论
所有情况下方框中三个数的和均为3的倍数。选项中只有2022是3的倍数($2022÷3=674$)。
B
设中间数为$x$,则三个数为$x-1$,$x$,$x+1$,和为$3x$,是3的倍数。
情况2:垂直方框(三个数在同一列)
每行8个数,设中间数为$x$,则三个数为$x-8$,$x$,$x+8$,和为$3x$,是3的倍数。
情况3:右倾对角线方框(左上-右下)
设中间数为$x$,则三个数为$x-9$,$x$,$x+9$,和为$3x$,是3的倍数。
情况4:左倾对角线方框(右上-左下)
设中间数为$x$,则三个数为$x-7$,$x$,$x+7$,和为$3x$,是3的倍数。
结论
所有情况下方框中三个数的和均为3的倍数。选项中只有2022是3的倍数($2022÷3=674$)。
B