5. 已知 $ x^2 - xy = - 3$,$ 2xy - y^2 = - 8$,则 $ 2x^2 + 4xy - 3y^2$ 的值为(
A.$-30$
B.$-11$
C.5
D.18
A
)A.$-30$
B.$-11$
C.5
D.18
答案:A
解析:
已知$x^2 - xy = -3$,$2xy - y^2 = -8$。
$2(x^2 - xy)=2×(-3)$,即$2x^2 - 2xy = -6$。
$3(2xy - y^2)=3×(-8)$,即$6xy - 3y^2 = -24$。
$2x^2 + 4xy - 3y^2=(2x^2 - 2xy)+(6xy - 3y^2)=-6 + (-24)=-30$
A
$2(x^2 - xy)=2×(-3)$,即$2x^2 - 2xy = -6$。
$3(2xy - y^2)=3×(-8)$,即$6xy - 3y^2 = -24$。
$2x^2 + 4xy - 3y^2=(2x^2 - 2xy)+(6xy - 3y^2)=-6 + (-24)=-30$
A
6. 已知 $ m = - 1$,则 $-2m - 1$ 的值为
1
。答案:1
解析:
当$m = -1$时,$-2m - 1=-2×(-1)-1=2 - 1=1$。
1
1
7. 已知 $ |n - 2| + (m + 3)^2 = 0$,则 $ m^n$ 的值等于
9
。答案:9
解析:
因为$|n - 2| \geq 0$,$(m + 3)^2 \geq 0$,且$|n - 2| + (m + 3)^2 = 0$,所以$|n - 2| = 0$,$(m + 3)^2 = 0$。
由$|n - 2| = 0$,得$n - 2 = 0$,解得$n = 2$。
由$(m + 3)^2 = 0$,得$m + 3 = 0$,解得$m = -3$。
则$m^n = (-3)^2 = 9$。
9
由$|n - 2| = 0$,得$n - 2 = 0$,解得$n = 2$。
由$(m + 3)^2 = 0$,得$m + 3 = 0$,解得$m = -3$。
则$m^n = (-3)^2 = 9$。
9
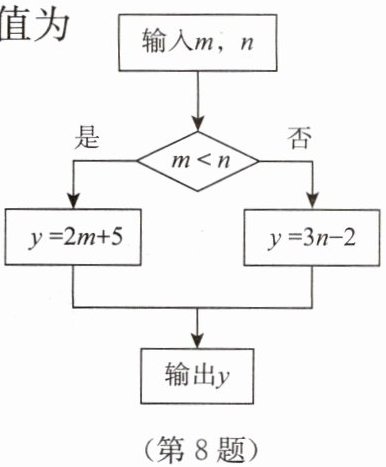
8. 根据如图所示的计算程序计算变量 $ y$ 的值,若输入 $ m = - 3$,$ n = - 2$,则输出 $ y$ 的值是
]
-1
。]

答案:-1
解析:
输入$m=-3$,$n=-2$,比较$m$与$n$大小:$-3 < -2$,满足$m < n$,则$y = 2m + 5$。代入$m=-3$,得$y=2×(-3)+5=-6 + 5=-1$。
-1
-1
9. 已知当 $ x = 3$ 时,代数式 $ ax^3 - bx + 5$ 的值为 $ 12$,则当 $ x = - 3$ 时,$ ax^3 - bx + 5$ 的值为
-2
。答案:-2
解析:
当$x = 3$时,$ax^3 - bx + 5 = 12$,则$ax^3 - bx = 12 - 5 = 7$,即$a \cdot 3^3 - b \cdot 3 = 7$,$27a - 3b = 7$。
当$x = -3$时,$ax^3 - bx + 5 = a \cdot (-3)^3 - b \cdot (-3) + 5 = -27a + 3b + 5 = -(27a - 3b) + 5$。
将$27a - 3b = 7$代入,得$-7 + 5 = -2$。
-2
当$x = -3$时,$ax^3 - bx + 5 = a \cdot (-3)^3 - b \cdot (-3) + 5 = -27a + 3b + 5 = -(27a - 3b) + 5$。
将$27a - 3b = 7$代入,得$-7 + 5 = -2$。
-2
10. 幻方最早起源于我国,古人称之为纵横图。如图所示的幻方中,每一行、每一列及各条对角线上的三个数之和均相等,则 $ x - y$ 的值为
]

-2
。]

答案:-2
11. A,B两地相距 $ s\ km$,甲、乙两人驾车分别以 $ a\ km/h$,$ b\ km/h$ 的速度从A地到B地,且甲用的时间较少。
(1)用代数式表示甲比乙少用的时间;
(2)当 $ s = 180$,$ a = 72$,$ b = 60$ 时,求(1)中代数式的值,并说明这个值表示的实际意义。
(1)用代数式表示甲比乙少用的时间;
(2)当 $ s = 180$,$ a = 72$,$ b = 60$ 时,求(1)中代数式的值,并说明这个值表示的实际意义。
答案:(1)$\left( \frac{s}{b}-\frac{s}{a} \right)$h. (2)因为$s=180$,$a=72$,$b=60$,所以(1)中代数式的值为$\frac{180}{60}-\frac{180}{72}=3-2.5=0.5$(h).这个值表示的实际意义是甲从A地到B地用的时间比乙少0.5小时.
解析:
(1)$\left( \frac{s}{b}-\frac{s}{a} \right)h$
(2)当$s=180$,$a=72$,$b=60$时,$\frac{180}{60}-\frac{180}{72}=3 - 2.5=0.5$。这个值表示甲从A地到B地比乙少用的时间为$0.5h$。
(2)当$s=180$,$a=72$,$b=60$时,$\frac{180}{60}-\frac{180}{72}=3 - 2.5=0.5$。这个值表示甲从A地到B地比乙少用的时间为$0.5h$。
12. 如图,在一个底为 $ a$,高为 $ h$ 的三角形铁皮上剪去一个半径为 $ r$ 的半圆。
(1)用含 $ a$,$ h$,$ r$ 的代数式表示剩下铁皮(阴影部分)的面积 $ S$。
(2)请求出当 $ a = 10$,$ h = 8$,$ r = 2$ 时,$ S$ 的取值($\pi$ 取 $ 3.14$)。
]

(1)用含 $ a$,$ h$,$ r$ 的代数式表示剩下铁皮(阴影部分)的面积 $ S$。
(2)请求出当 $ a = 10$,$ h = 8$,$ r = 2$ 时,$ S$ 的取值($\pi$ 取 $ 3.14$)。
]

答案:(1)$S=S_{三角形}-S_{半圆}=\frac{1}{2}ah-\frac{1}{2}\pi r^{2}$;(2)$S=\frac{1}{2}ah-\frac{1}{2}\pi r^{2}=\frac{1}{2}×10×8-\frac{1}{2}\pi×2^{2}=40-2\pi=33.72$.
解析:
(1)$S=\frac{1}{2}ah-\frac{1}{2}\pi r^{2}$;
(2)当$a = 10$,$h = 8$,$r = 2$时,$S=\frac{1}{2}×10×8-\frac{1}{2}×3.14×2^{2}=40 - 6.28=33.72$。
(2)当$a = 10$,$h = 8$,$r = 2$时,$S=\frac{1}{2}×10×8-\frac{1}{2}×3.14×2^{2}=40 - 6.28=33.72$。
若 $ x^2 + x - 2 = 0$,求下列各代数式的值。
(1)$ x^2 + x + 2026$;
(2)$ x^3 + 2x^2 - x + 2026$。
(1)$ x^2 + x + 2026$;
(2)$ x^3 + 2x^2 - x + 2026$。
答案:(1)2028;(2)2028.
解析:
(1)因为$x^2 + x - 2 = 0$,所以$x^2 + x = 2$,则$x^2 + x + 2026 = 2 + 2026 = 2028$。
(2)因为$x^2 + x = 2$,所以$x^3 + 2x^2 - x + 2026 = x(x^2 + x) + x^2 - x + 2026 = 2x + x^2 - x + 2026 = x^2 + x + 2026 = 2 + 2026 = 2028$。
(2)因为$x^2 + x = 2$,所以$x^3 + 2x^2 - x + 2026 = x(x^2 + x) + x^2 - x + 2026 = 2x + x^2 - x + 2026 = x^2 + x + 2026 = 2 + 2026 = 2028$。