7. 若 $ m$,$n$ 互为相反数,$ p$,$ q$ 互为倒数,则 $-2026(m + n) + \frac{3}{pq}$ 的值是
3
。答案:3
解析:
因为$m$,$n$互为相反数,所以$m + n=0$;因为$p$,$q$互为倒数,所以$pq = 1$。
则$-2026(m + n)+\frac{3}{pq}=-2026×0+\frac{3}{1}=0 + 3=3$。
3
则$-2026(m + n)+\frac{3}{pq}=-2026×0+\frac{3}{1}=0 + 3=3$。
3
8. 已知 $ |a| = 3$,$ |b - 1| = 5$,且 $ a > b$,则 $ a + b$ 的值为
-7或-1
。答案:-7或-1
解析:
因为$|a| = 3$,所以$a = 3$或$a=-3$;
因为$|b - 1| = 5$,所以$b-1=5$或$b-1=-5$,解得$b = 6$或$b=-4$。
又因为$a>b$,
当$a = 3$时,$b=-4$($b = 6$不满足$3>6$),此时$a + b=3+(-4)=-1$;
当$a=-3$时,$b=-4$($b = 6$不满足$-3>6$),此时$a + b=-3+(-4)=-7$。
综上,$a + b$的值为$-7$或$-1$。
因为$|b - 1| = 5$,所以$b-1=5$或$b-1=-5$,解得$b = 6$或$b=-4$。
又因为$a>b$,
当$a = 3$时,$b=-4$($b = 6$不满足$3>6$),此时$a + b=3+(-4)=-1$;
当$a=-3$时,$b=-4$($b = 6$不满足$-3>6$),此时$a + b=-3+(-4)=-7$。
综上,$a + b$的值为$-7$或$-1$。
问题 如图,用“8字砖”铺设地面,1块地砖有2个正方形,2块地砖拼得5个正方形,3块地砖拼得8个正方形……照此规律拼下去。
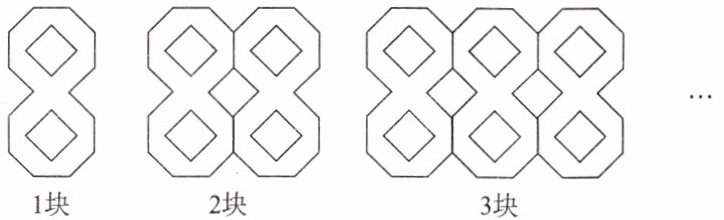
(1)请用含 $ n$ 的代数式表示:$ n$ 块地砖拼得的正方形的个数为
(2)求当 $ n = 20$ 时,拼得的正方形的个数;
(3)若 $ m$ 块地砖拼得的正方形的个数是 $ 170$,求 $ m$ 的值。
名师指导
先从前面几个具体的图形数量发现并得出具有相同规律的代数式,再总结归纳即可。
解题示范(学生在教师指导下,独立完成)
解:

(1)请用含 $ n$ 的代数式表示:$ n$ 块地砖拼得的正方形的个数为
3n - 1
个;(2)求当 $ n = 20$ 时,拼得的正方形的个数;
(3)若 $ m$ 块地砖拼得的正方形的个数是 $ 170$,求 $ m$ 的值。
名师指导
先从前面几个具体的图形数量发现并得出具有相同规律的代数式,再总结归纳即可。
解题示范(学生在教师指导下,独立完成)
解:
答案:(1)设$n$块地砖拼得的正方形的个数为$a_{n}$。
观察可得:
$a_{1}=2 = 3×1 - 1$;
$a_{2}=5 = 3×2 - 1$;
$a_{3}=8 = 3×3 - 1$;
$\cdots$
则$n$块地砖拼得的正方形的个数为$3n - 1$。
(2)当$n = 20$时,
$a_{20}=3×20 - 1=59$(个)
(3)当$a_{m}=170$时,
$3m - 1 = 170$,
$3m=171$,
$m = 57$。
综上,答案依次为:(1)$3n - 1$;(2)$59$个;(3)$57$。
观察可得:
$a_{1}=2 = 3×1 - 1$;
$a_{2}=5 = 3×2 - 1$;
$a_{3}=8 = 3×3 - 1$;
$\cdots$
则$n$块地砖拼得的正方形的个数为$3n - 1$。
(2)当$n = 20$时,
$a_{20}=3×20 - 1=59$(个)
(3)当$a_{m}=170$时,
$3m - 1 = 170$,
$3m=171$,
$m = 57$。
综上,答案依次为:(1)$3n - 1$;(2)$59$个;(3)$57$。
1. 若 $ a$,$ b$ 互为相反数($ a\neq0$),则 $\frac{b}{a} + 3$ 的值为(
A.2
B.0
C.$\pm1$
D.0 或 2
A
)A.2
B.0
C.$\pm1$
D.0 或 2
答案:A
解析:
因为$a$,$b$互为相反数($a\neq0$),所以$b=-a$。
则$\frac{b}{a}=\frac{-a}{a}=-1$。
所以$\frac{b}{a}+3=-1 + 3=2$。
A
则$\frac{b}{a}=\frac{-a}{a}=-1$。
所以$\frac{b}{a}+3=-1 + 3=2$。
A
2. 若 $ x - 3y = 4$,则 $ 3 - 2x + 6y$ 的值是(
A.$-5$
B.$-1$
C.8
D.11
A
)A.$-5$
B.$-1$
C.8
D.11
答案:A
解析:
已知$x - 3y = 4$,则$-2x + 6y = -2(x - 3y) = -2×4 = -8$,所以$3 - 2x + 6y = 3 + (-8) = -5$。
A
A
3. 如图,长和宽分别为 $ a$,$ b$ 的长方形的周长为 $ 14$,面积为 $ 10$,则 $ ab(a + b)$ 的值为(

A.140
B.70
C.35
D.24
B
)
A.140
B.70
C.35
D.24
答案:B
解析:
长方形周长为 $2(a + b) = 14$,则 $a + b = 7$;面积为 $ab = 10$。$ab(a + b) = 10 × 7 = 70$。
B
B
4. 一组数 $ 2$,$1$,$5$,$x$,$17$,$y$,$65$,满足“前两个数依次为 $ a$,$ b$,紧随其后的第三个数是 $ 2a + b$”,例如这组数中的第三个数“5”是由“$ 2×2 + 1$”得到的,那么这组数中 $ y$ 表示的数为(
A.27
B.11
C.31
D.41
C
)A.27
B.11
C.31
D.41
答案:C
解析:
由题意得:
第三个数:$2×2 + 1 = 5$
第四个数:$2×1 + 5 = x$,解得$x = 7$
第五个数:$2×5 + 7 = 17$
第六个数:$2×7 + 17 = y$,解得$y = 31$
第七个数:$2×17 + 31 = 65$
结论:$y = 31$
C
第三个数:$2×2 + 1 = 5$
第四个数:$2×1 + 5 = x$,解得$x = 7$
第五个数:$2×5 + 7 = 17$
第六个数:$2×7 + 17 = y$,解得$y = 31$
第七个数:$2×17 + 31 = 65$
结论:$y = 31$
C