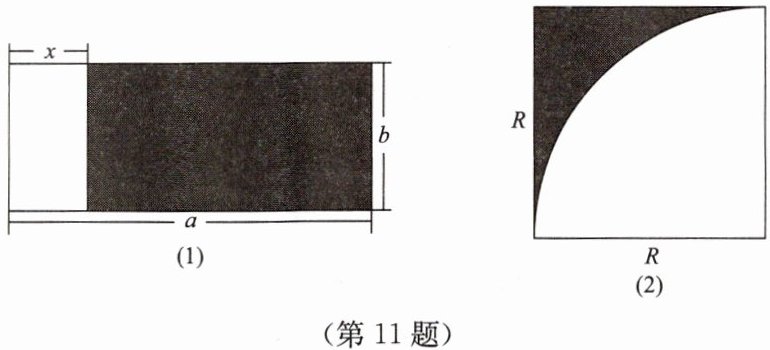
11. 用字母表示图中阴影部分的面积。
]
]

答案:
(1)$ab-bx$;
(2)$R^{2}-\frac{1}{4}\pi R^{2}$
(1)$ab-bx$;
(2)$R^{2}-\frac{1}{4}\pi R^{2}$
粗心的小倩在放学回家后,发现把数学练习册忘在教室了,担心教室关门,于是她跑步到学校取了练习册,再步行回家(取书时间忽略不计)。已知跑步速度为$x$,步行速度为$y$,则她往返一趟的平均速度是(
A.$x$
B.$y$
C.$\frac{x + y}{2}$
D.$\frac{2xy}{x + y}$
D
)A.$x$
B.$y$
C.$\frac{x + y}{2}$
D.$\frac{2xy}{x + y}$
答案:D
解析:
设家到学校的路程为$s$。
跑步到学校的时间为$\frac{s}{x}$,步行回家的时间为$\frac{s}{y}$。
往返总路程为$2s$,总时间为$\frac{s}{x}+\frac{s}{y}=\frac{s(x + y)}{xy}$。
平均速度$=\frac{总路程}{总时间}=\frac{2s}{\frac{s(x + y)}{xy}}=\frac{2xy}{x + y}$。
D
跑步到学校的时间为$\frac{s}{x}$,步行回家的时间为$\frac{s}{y}$。
往返总路程为$2s$,总时间为$\frac{s}{x}+\frac{s}{y}=\frac{s(x + y)}{xy}$。
平均速度$=\frac{总路程}{总时间}=\frac{2s}{\frac{s(x + y)}{xy}}=\frac{2xy}{x + y}$。
D
1. 若 $ a = 4$,$ b = - 2$,则代数式 $ a - ab$ 的值为(
A.14
B.24
C.20
D.12
D
)A.14
B.24
C.20
D.12
答案:D
解析:
当$a = 4$,$b=-2$时,$a - ab=4-4×(-2)=4 + 8=12$。
D
D
2. 若 $ x$ 的相反数是 $-3$,则代数式 $ 2x - 1$ 的值是(
A.$-7$
B.$-5$
C.5
D.7
C
)A.$-7$
B.$-5$
C.5
D.7
答案:C
解析:
因为$x$的相反数是$-3$,所以$x = 3$。将$x = 3$代入$2x - 1$,得$2×3 - 1 = 6 - 1 = 5$。
C
C
3. 代数式 $ kx + b$ 中,当 $ x$ 取值分别为 $-1$,$0$,$1$,$2$ 时,对应代数式的值如下表:

则 $ k + b$ 的值为(
A.$-1$
B.1
C.3
D.5

则 $ k + b$ 的值为(
C
)A.$-1$
B.1
C.3
D.5
答案:C
解析:
当$x=0$时,$kx + b = 1$,即$k×0 + b=1$,解得$b = 1$。
当$x=1$时,$kx + b = 3$,将$b = 1$代入得$k×1 + 1=3$,解得$k=2$。
所以$k + b=2 + 1=3$。
C
当$x=1$时,$kx + b = 3$,将$b = 1$代入得$k×1 + 1=3$,解得$k=2$。
所以$k + b=2 + 1=3$。
C
4. 已知 $ |3m - 12| + (4 + n)^2 = 0$,则 $ 2m - n = $(
A.8
B.12
C.4
D.$-4$
B
)A.8
B.12
C.4
D.$-4$
答案:B
解析:
因为$|3m - 12| + (4 + n)^2 = 0$,且$|3m - 12| \geq 0$,$(4 + n)^2 \geq 0$,所以$3m - 12 = 0$,$4 + n = 0$。解得$m = 4$,$n = -4$。则$2m - n = 2×4 - (-4) = 8 + 4 = 12$。
B
B
5. 若 $ x$ 的相反数是 $ 2$,$ |y| = 5$,且 $ x + y > 0$,则 $ x - y$ 的值是(
A.3
B.3 或 $-7$
C.$-3$ 或 $-7$
D.$-7$
D
)A.3
B.3 或 $-7$
C.$-3$ 或 $-7$
D.$-7$
答案:D
解析:
因为$x$的相反数是$2$,所以$x=-2$。
因为$|y| = 5$,所以$y = 5$或$y=-5$。
当$y = 5$时,$x + y=-2 + 5=3>0$,符合条件,此时$x - y=-2-5=-7$;
当$y=-5$时,$x + y=-2+(-5)=-7<0$,不符合条件,舍去。
综上,$x - y=-7$。
D
因为$|y| = 5$,所以$y = 5$或$y=-5$。
当$y = 5$时,$x + y=-2 + 5=3>0$,符合条件,此时$x - y=-2-5=-7$;
当$y=-5$时,$x + y=-2+(-5)=-7<0$,不符合条件,舍去。
综上,$x - y=-7$。
D
6. 某地海拔高度 $ h(km)$ 与温度 $ T(^{\circ}C)$ 的关系可用 $ T = 20 - 6h$ 来表示,则该地区某海拔高度为 $ 2000m$ 的山顶上的温度为
8℃
。答案:8℃
解析:
2000m=2km,将$h = 2$代入$T = 20 - 6h$,得$T = 20 - 6×2 = 20 - 12 = 8$,所以温度为$8^{\circ}C$。