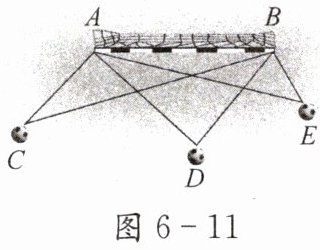
1. 如图6-11,三名足球运动员在不同的位置射门,你觉得哪个位置射门进球的可能性最大?哪个位置射门进球的可能性最小?与同伴交流.

答案:结合图形可知:
E点离球门距离最近,进球的可能性最大;
C点离球门距离最远,进球的可能性最小。
E点离球门距离最近,进球的可能性最大;
C点离球门距离最远,进球的可能性最小。
2. 任意画一个角,和同桌比一比你们画的角哪个大,哪个小.你采用了怎样的方法比较两个角的大小?
答案:解:1.中间位置的运动员射门进球的可能性最大,左边位置的运动员射门进球的可能性最小;
射门的角度越大,进球的可能性就越大
2.用度量的方法或叠合的方法
射门的角度越大,进球的可能性就越大
2.用度量的方法或叠合的方法
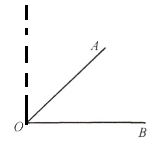
如图6-12,已知∠AOB,如何用量角器画一个与∠AOB相等的角?画一画.如果只用直尺和圆规,你能否解决这个问题?试一试.(可以仿照课本中的例3)


答案:

1. 在透明纸上画一个角,试着把这个角分成两个相等的角,说说你的做法.
答案:解:可以将纸对折使得角的两边重合,折痕就将这个角平分成两个相等的角
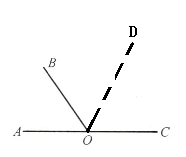
2. (1)类比线段中点的定义,请你说说什么是角的平分线?试着画出图6-13中∠AOB的平分线OC.那么∠AOC= ∠______= ______∠AOB,∠AOB= ______∠AOC= ______∠BOC.
(2)如图6-13,若∠AOB= 55°,请你画出∠BOC的平分线OD,并计算∠AOD的度数.

(2)如图6-13,若∠AOB= 55°,请你画出∠BOC的平分线OD,并计算∠AOD的度数.

答案:
BOC
$\frac {1}{2}$
2
2
解:∵OD平分∠BOC,∴∠BOD=∠COD
∠BOC=180°-∠AOB=125°
∴$∠BOD=∠COD=\frac {1}{2}∠BOC=62.5°$
∴∠AOD=∠AOB+∠BOD=117.5°
解:如果从角的顶点出发的一条射线把这个角分成两个相等的角,这条射线叫作这个角的角平分线
BOC
$\frac {1}{2}$
2
2
解:∵OD平分∠BOC,∴∠BOD=∠COD
∠BOC=180°-∠AOB=125°
∴$∠BOD=∠COD=\frac {1}{2}∠BOC=62.5°$
∴∠AOD=∠AOB+∠BOD=117.5°
解:如果从角的顶点出发的一条射线把这个角分成两个相等的角,这条射线叫作这个角的角平分线

1. 下列说法中,正确的是(
A.角的两边画得越长,角就越大
B.两个角的一边重合,另外两边组成的图形是这两个角的和
C.从角的顶点出发的一条射线叫作角的平分线
D.从角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫作角的平分线
D
)A.角的两边画得越长,角就越大
B.两个角的一边重合,另外两边组成的图形是这两个角的和
C.从角的顶点出发的一条射线叫作角的平分线
D.从角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫作角的平分线
答案:D
解析:
A选项错误,因为角的大小与角的两边画得长短无关,只与两边张开的程度有关;
B选项错误,两个角的和并不是由一边重合,另外两边组成的图形,而是两个角相加的结果;
C选项错误,从角的顶点出发的一条射线并不直接称为角的平分线,必须这条射线把这个角分成两个相等的角,才能称为角的平分线;
D选项正确,它准确地描述了角的平分线的定义,即从角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫作角的平分线。
B选项错误,两个角的和并不是由一边重合,另外两边组成的图形,而是两个角相加的结果;
C选项错误,从角的顶点出发的一条射线并不直接称为角的平分线,必须这条射线把这个角分成两个相等的角,才能称为角的平分线;
D选项正确,它准确地描述了角的平分线的定义,即从角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫作角的平分线。