2. 如图,下列说理中,正确的是(
A.因为∠A+∠D= 180°,所以AD//BC
B.因为∠C+∠D= 180°,所以AB//CD
C.因为∠A+∠D= 180°,所以AB//CD
D.因为∠A+∠C= 180°,所以AB//CD
C
)A.因为∠A+∠D= 180°,所以AD//BC
B.因为∠C+∠D= 180°,所以AB//CD
C.因为∠A+∠D= 180°,所以AB//CD
D.因为∠A+∠C= 180°,所以AB//CD
答案:C
解析:
选项A:因为$\angle A + \angle D = 180^\circ$,同旁内角互补,两直线平行,所以应该是$AB// CD$,而不是$AD// BC$,所以A选项错误;
选项B:因为$\angle C + \angle D = 180^\circ$,同旁内角互补,两直线平行,所以应该是$AD// BC$,而不是$AB// CD$,所以B选项错误;
选项C:因为$\angle A + \angle D = 180^\circ$,同旁内角互补,两直线平行,所以$AB// CD$,C选项正确;
选项D:$\angle A$与$\angle C$是同旁内角,但是不能通过这两个角的关系来判断$AB// CD$,所以D选项错误。
选项B:因为$\angle C + \angle D = 180^\circ$,同旁内角互补,两直线平行,所以应该是$AD// BC$,而不是$AB// CD$,所以B选项错误;
选项C:因为$\angle A + \angle D = 180^\circ$,同旁内角互补,两直线平行,所以$AB// CD$,C选项正确;
选项D:$\angle A$与$\angle C$是同旁内角,但是不能通过这两个角的关系来判断$AB// CD$,所以D选项错误。
3. 如图,点E在CD的延长线上,下列条件中不能推出AC//BD的是(
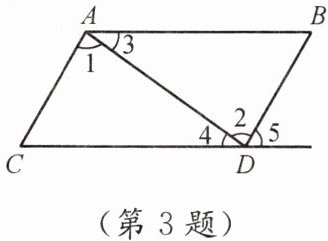
A.∠1= ∠2
B.∠3= ∠4
C.∠5= ∠C
D.∠C+∠BDC= 180°
C
)
A.∠1= ∠2
B.∠3= ∠4
C.∠5= ∠C
D.∠C+∠BDC= 180°
答案:C
解析:
选项A:∠1和∠2是内错角,根据内错角相等,两直线平行可判断$AC// BD$。
选项B:∠3和∠4是内错角,根据内错角相等,两直线平行可判断$AC// BD$。
选项C:∠5和∠C不是同位角、内错角,也不是同旁内角,不能根据它们相等判断$AC// BD$。
选项D:∠C和∠BDC是同旁内角,根据同旁内角互补,两直线平行可判断$AC// BD$。
选项B:∠3和∠4是内错角,根据内错角相等,两直线平行可判断$AC// BD$。
选项C:∠5和∠C不是同位角、内错角,也不是同旁内角,不能根据它们相等判断$AC// BD$。
选项D:∠C和∠BDC是同旁内角,根据同旁内角互补,两直线平行可判断$AC// BD$。
4. 如图,∠1+∠3= 180°,能否得出AB//CD?为什么?


答案:解:可以,理由:
易知,∠BGH=∠1,∠GHD=∠3
又∵∠1+∠3=180°,∴∠BGH+∠GHD=180°
∴AB//CD
易知,∠BGH=∠1,∠GHD=∠3
又∵∠1+∠3=180°,∴∠BGH+∠GHD=180°
∴AB//CD
解:因为AF平分∠DAB,
所以
又因为CE平分∠DCB,
所以∠FCE=
因为∠DAB= ∠DCB(
所以∠FAE= ∠FCE.
因为∠FCE= ∠CEB,
所以
所以AF//CE(
所以
∠FAE
= ∠DAB(角平分线定义
).又因为CE平分∠DCB,
所以∠FCE=
$\frac{1}{2}∠FCB$
(角平分线定义
).因为∠DAB= ∠DCB(
已知
),所以∠FAE= ∠FCE.
因为∠FCE= ∠CEB,
所以
∠FAE
= ∠CEB
.所以AF//CE(
同位角相等,两直线平行
).答案:∠FAE
角平分线定义
$\frac{1}{2}∠FCB$
角平分线定义
已知
∠FAE
∠CEB
同位角相等,两直线平行
角平分线定义
$\frac{1}{2}∠FCB$
角平分线定义
已知
∠FAE
∠CEB
同位角相等,两直线平行
2. 如图,GH分别交AB,CD于点E,F,∠AEF= ∠EFD.

(1)试写出AB//CD的依据.
(2)若ME是∠AEF的平分线,FN是∠EFD的平分线,则EM,FN平行吗?若平行,请说明理由.

(1)试写出AB//CD的依据.
(2)若ME是∠AEF的平分线,FN是∠EFD的平分线,则EM,FN平行吗?若平行,请说明理由.
答案:解:(1)内错角相等,两直线平行
(2)ME//FN,理由如下:
因为ME是∠AEF的平分线,所以$∠MEF=\frac{1}{2}∠AEF$
同理,$∠NFE=\frac{1}{2}∠EFD$
因为∠AEF=∠EFD,所以∠MEF=∠EFN
所以ME//FN
(2)ME//FN,理由如下:
因为ME是∠AEF的平分线,所以$∠MEF=\frac{1}{2}∠AEF$
同理,$∠NFE=\frac{1}{2}∠EFD$
因为∠AEF=∠EFD,所以∠MEF=∠EFN
所以ME//FN