1. (1) 什么是多边形的对角线?
(2) 将表格补充完整:
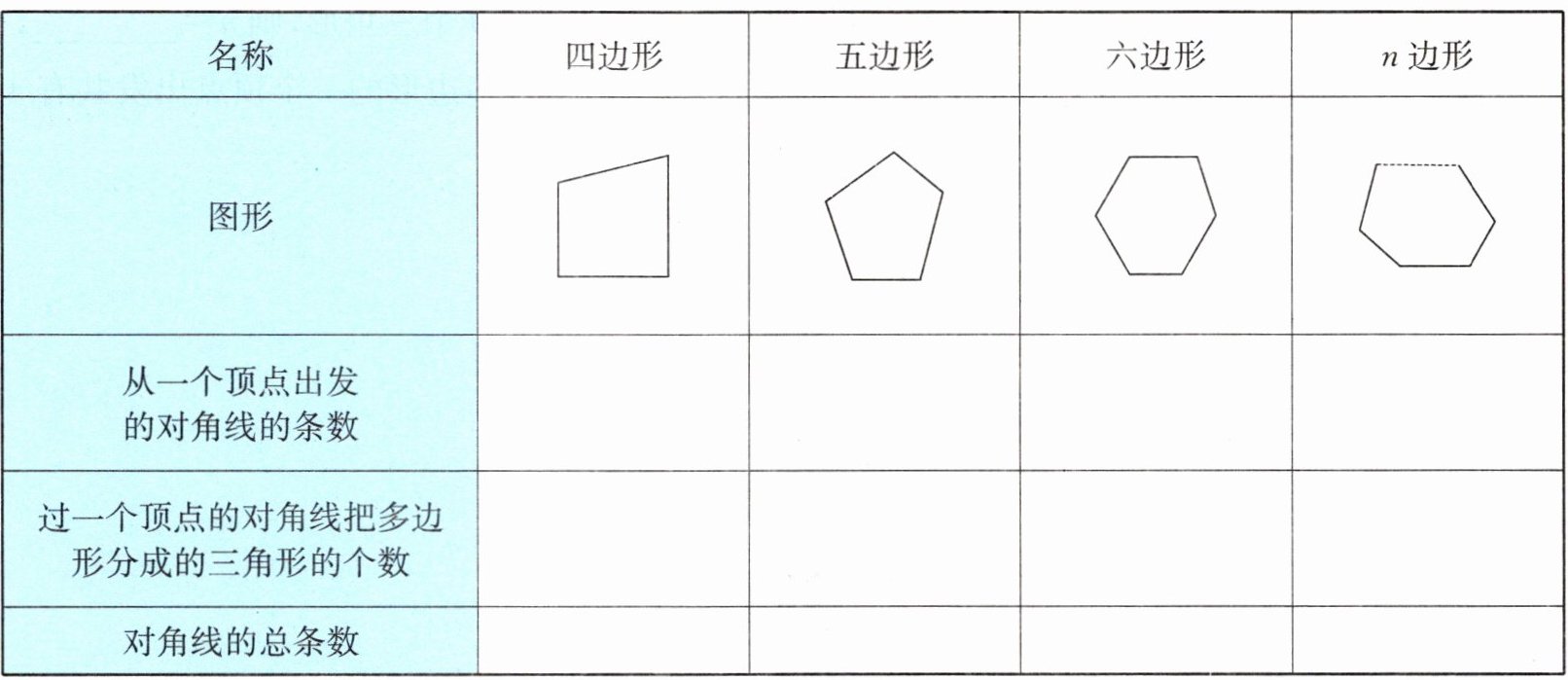
(2) 将表格补充完整:

答案:
(1) 连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
(2)
|名称|四边形|五边形|六边形|n边形|
| ---- | ---- | ---- | ---- | ---- |
|图形|  |  |  |  |
|从一个顶点出发的对角线的条数| 1 | 2 | 3 | $n - 3$ |
|过一个顶点的对角线把多边形分成的三角形的个数| 2 | 3 | 4 | $n - 2$ |
|对角线的总条数| 2 | 5 | 9 | $\frac{n(n - 3)}{2}$ |
(1) 连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
(2)
|名称|四边形|五边形|六边形|n边形|
| ---- | ---- | ---- | ---- | ---- |
|图形|  |  |  |  |
|从一个顶点出发的对角线的条数| 1 | 2 | 3 | $n - 3$ |
|过一个顶点的对角线把多边形分成的三角形的个数| 2 | 3 | 4 | $n - 2$ |
|对角线的总条数| 2 | 5 | 9 | $\frac{n(n - 3)}{2}$ |
2. 归纳:(1) 从n边形一个顶点出发的对角线有
(2) 过n边形一个顶点的对角线把n边形分成
(3) n边形共有
n-3
条;(2) 过n边形一个顶点的对角线把n边形分成
n-2
个三角形;(3) n边形共有
n(n-3)/2
条对角线.(n≥3)答案:(1) n-3
(2) n-2
(3) n(n-3)/2
(2) n-2
(3) n(n-3)/2
解析:
(1) 从n边形的一个顶点出发,除了此顶点本身和相邻的两个顶点不能作为对角线的终点外,其余(n-3)个顶点均可作为对角线的终点。因此,从n边形一个顶点出发的对角线有(n-3)条。
(2) 从n边形的一个顶点出发的对角线将n边形划分为若干个三角形。由于每条对角线都将一个顶点与其他非相邻的顶点相连,因此会划分出(n-2)个三角形。可以通过观察或推理得出,每增加一个顶点,就会多出一个三角形。
(3) n边形中的对角线总数可以通过组合数学的方法计算。每个顶点都可以发出(n-3)条对角线,由于n边形有n个顶点,因此总共有n(n-3)条对角线被计算了两次(每条对角线连接两个顶点)。所以,n边形的对角线总数为n(n-3)/2。
(2) 从n边形的一个顶点出发的对角线将n边形划分为若干个三角形。由于每条对角线都将一个顶点与其他非相邻的顶点相连,因此会划分出(n-2)个三角形。可以通过观察或推理得出,每增加一个顶点,就会多出一个三角形。
(3) n边形中的对角线总数可以通过组合数学的方法计算。每个顶点都可以发出(n-3)条对角线,由于n边形有n个顶点,因此总共有n(n-3)条对角线被计算了两次(每条对角线连接两个顶点)。所以,n边形的对角线总数为n(n-3)/2。
3. (1) 观察图6-32中的图形,它们的边、角有什么特点?在横线上填写各个图形的名称:

(2) 请用自己的语言说明什么叫作正多边形:

三角形;四边形;五边形;六边形
(2) 请用自己的语言说明什么叫作正多边形:
各条边都相等,各个角也都相等
的多边形叫作正多边形.答案:
(1) 从左到右各个图形的名称为:三角形;四边形;五边形;六边形。
(2) 各条边都相等,各个角也都相等。
(1) 从左到右各个图形的名称为:三角形;四边形;五边形;六边形。
(2) 各条边都相等,各个角也都相等。
4. (1) 一个多边形的边都相等,它的内角一定都相等吗?请举例说明.
(2) 一个多边形的内角都相等,它的边一定都相等吗?请举例说明.
(2) 一个多边形的内角都相等,它的边一定都相等吗?请举例说明.
答案:(1) 一个多边形的边都相等,它的内角不一定都相等。
举例:菱形。菱形的四条边都相等,但它的内角不一定都相等(只有相对的两个内角相等,相邻的内角不一定相等)。
(2) 一个多边形的内角都相等,它的边不一定都相等。
举例:长方形。长方形的四个内角都是$90^\circ$,都是相等的,但它的长和宽不一定相等。
举例:菱形。菱形的四条边都相等,但它的内角不一定都相等(只有相对的两个内角相等,相邻的内角不一定相等)。
(2) 一个多边形的内角都相等,它的边不一定都相等。
举例:长方形。长方形的四个内角都是$90^\circ$,都是相等的,但它的长和宽不一定相等。
5. 结论:正多边形必须满足
所有的边相等
,所有的内角相等
.答案:所有的边相等,所有的内角相等
解析:
正多边形是一个几何图形,其中所有的边都相等且所有的内角都相等。这两个条件必须同时满足,才能称为正多边形。
1. 下列说法正确的是(
A.各角都相等的多边形是正多边形
B.各边都相等的多边形是正多边形
C.正方形是正多边形
D.经过n边形的一个顶点可画(n-2)条对角线
C
)A.各角都相等的多边形是正多边形
B.各边都相等的多边形是正多边形
C.正方形是正多边形
D.经过n边形的一个顶点可画(n-2)条对角线
答案:C
解析:
A. 各角都相等的多边形不一定是正多边形,因为正多边形不仅要求各角相等,还要求各边相等。所以A选项错误。
B. 各边都相等的多边形不一定是正多边形,因为正多边形不仅要求各边相等,还要求各角相等。所以B选项错误。
C. 正方形各边相等且各角都是直角,满足正多边形的定义,所以C选项正确。
D. 对于n边形,经过一个顶点可画的对角线数量是(n-3),因为与该顶点相邻的两个顶点和该顶点自身不能构成对角线。所以D选项错误。
B. 各边都相等的多边形不一定是正多边形,因为正多边形不仅要求各边相等,还要求各角相等。所以B选项错误。
C. 正方形各边相等且各角都是直角,满足正多边形的定义,所以C选项正确。
D. 对于n边形,经过一个顶点可画的对角线数量是(n-3),因为与该顶点相邻的两个顶点和该顶点自身不能构成对角线。所以D选项错误。