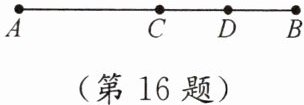
16. (10分)如图,C是线段AB的中点,D是线段BC的中点,已知图中所有线段的长度之和为39,求线段BC的长.

答案:
解:由题,AC+CD+BD+AD+BC+AB=39
即3AB+CD=39
∵C是AB中点,D是BC中点
∴AC=BC,BD=CD
∴AB=2BC=4CD
∴可求得CD=3,AB=12
∴$BC=\frac {1}{2}AB=6$
解:由题,AC+CD+BD+AD+BC+AB=39
即3AB+CD=39
∵C是AB中点,D是BC中点
∴AC=BC,BD=CD
∴AB=2BC=4CD
∴可求得CD=3,AB=12
∴$BC=\frac {1}{2}AB=6$
17. (12分)(1) 如图①,将两块三角板的直角顶点C叠放在一起,并回答下列问题:
① ∠ACE与∠DCB的度数有何数量关系? 说明理由;
② ∠ACB与∠DCE的度数有何数量关系? 说明理由.
(2) 如图②,若将两个三角板的60°角和90°角的顶点A叠放在一起,将三角板ADE绕点A旋转,旋转过程中三角板ADE的边AD始终在∠BAC的内部,试探索:在旋转过程中,∠CAE与∠BAD的度数之差是否发生变化? 若不变,求出这个差值;若变化,求出差的变化范围.

① ∠ACE与∠DCB的度数有何数量关系? 说明理由;
② ∠ACB与∠DCE的度数有何数量关系? 说明理由.
(2) 如图②,若将两个三角板的60°角和90°角的顶点A叠放在一起,将三角板ADE绕点A旋转,旋转过程中三角板ADE的边AD始终在∠BAC的内部,试探索:在旋转过程中,∠CAE与∠BAD的度数之差是否发生变化? 若不变,求出这个差值;若变化,求出差的变化范围.

答案:解:(1)①∠ACE=∠DCB,理由:
易知,∠ACD=∠ECB=90°
又∵∠ACE=90°-∠ECD,∠DCB=90°-∠ECD
∴∠ACE=∠DCB
②∠ACB+∠DCE=180°,理由:
∠ACB+∠DCE=∠ACD+∠DCB+∠ECD
=∠ACD+∠ECB=180°
(2)易求,∠CAE=∠DAE-∠DAC=90°-∠DAC
∠BAD=∠BAC-∠DAC=60°-∠DAC
∴∠CAE-∠BAD=30°
即这个差值不会变化为30°
易知,∠ACD=∠ECB=90°
又∵∠ACE=90°-∠ECD,∠DCB=90°-∠ECD
∴∠ACE=∠DCB
②∠ACB+∠DCE=180°,理由:
∠ACB+∠DCE=∠ACD+∠DCB+∠ECD
=∠ACD+∠ECB=180°
(2)易求,∠CAE=∠DAE-∠DAC=90°-∠DAC
∠BAD=∠BAC-∠DAC=60°-∠DAC
∴∠CAE-∠BAD=30°
即这个差值不会变化为30°