9. 37.34°=
37
°20
′24
″,134°13′30″=134.225
°.答案:37
20
24
134.225
20
24
134.225
解析:
对于 $37.34{^\circ}$,
首先,整数部分即为度数,即 $37{^\circ}$。
然后,小数部分 $0.34$ 转换为分,即 $0.34 × 60 = 20.4′$,
其中整数部分 $20$ 为分,即 $20′$,
小数部分 $0.4$ 再转换为秒,即 $0.4 × 60 = 24″$。
所以,$37.34{^\circ} = 37{^\circ}20′24″$。
对于 $134{^\circ}13′30″$,
首先,度数部分为 $134{^\circ}$。
然后,$13′$ 转换为度,即 $\frac{13}{60} = 0.2166...{^\circ}$,取小数点后三位为 $0.217{^\circ}$(由于秒数转换为度数会有更多小数位,但此处我们按题目要求取三位),
实际应保留更多小数位以确保后续加法的精度。
接着,$30″$ 转换为度,即 $\frac{30}{3600} = 0.0083...{^\circ}$,
同样地,我们取足够多的小数位(在这里至少到万分位以确保加法的准确性),即 $0.0083{^\circ}$。
将这三部分相加,得到 $134{^\circ} + 0.2166...{^\circ} + 0.0083{^\circ} = 134.225{^\circ}$(结果保留到千分位)。
但更精确的计算应为:
$134{^\circ}13′30″ = 134{^\circ} + \frac{13}{60}{^\circ} + \frac{30}{3600}{^\circ}$
$= 134{^\circ} + 0.216666...{^\circ} + 0.008333...{^\circ}$
$= 134.225{^\circ}$(四舍五入到千分位)
所以,$134{^\circ}13′30″ = 134.225{^\circ}$。
首先,整数部分即为度数,即 $37{^\circ}$。
然后,小数部分 $0.34$ 转换为分,即 $0.34 × 60 = 20.4′$,
其中整数部分 $20$ 为分,即 $20′$,
小数部分 $0.4$ 再转换为秒,即 $0.4 × 60 = 24″$。
所以,$37.34{^\circ} = 37{^\circ}20′24″$。
对于 $134{^\circ}13′30″$,
首先,度数部分为 $134{^\circ}$。
然后,$13′$ 转换为度,即 $\frac{13}{60} = 0.2166...{^\circ}$,取小数点后三位为 $0.217{^\circ}$(由于秒数转换为度数会有更多小数位,但此处我们按题目要求取三位),
实际应保留更多小数位以确保后续加法的精度。
接着,$30″$ 转换为度,即 $\frac{30}{3600} = 0.0083...{^\circ}$,
同样地,我们取足够多的小数位(在这里至少到万分位以确保加法的准确性),即 $0.0083{^\circ}$。
将这三部分相加,得到 $134{^\circ} + 0.2166...{^\circ} + 0.0083{^\circ} = 134.225{^\circ}$(结果保留到千分位)。
但更精确的计算应为:
$134{^\circ}13′30″ = 134{^\circ} + \frac{13}{60}{^\circ} + \frac{30}{3600}{^\circ}$
$= 134{^\circ} + 0.216666...{^\circ} + 0.008333...{^\circ}$
$= 134.225{^\circ}$(四舍五入到千分位)
所以,$134{^\circ}13′30″ = 134.225{^\circ}$。
10. 已知C是线段AD的中点,B是线段AC的中点,AD= 60,则BC=
15
.答案:15
解析:
因为C是线段AD的中点,AD=60,所以AC=$\frac{1}{2}$AD=$\frac{1}{2}×60=30$。
因为B是线段AC的中点,所以BC=$\frac{1}{2}$AC=$\frac{1}{2}×30=15$。
15
因为B是线段AC的中点,所以BC=$\frac{1}{2}$AC=$\frac{1}{2}×30=15$。
15
11. 如图,当剪刀口∠AOB增大15°时,∠COD增大
15
°.答案:
15
15
解析:
因为$\angle AOB$与$\angle COD$是对顶角,对顶角相等,所以当$\angle AOB$增大$15^{\circ}$时,$\angle COD$也增大$15^{\circ}$。
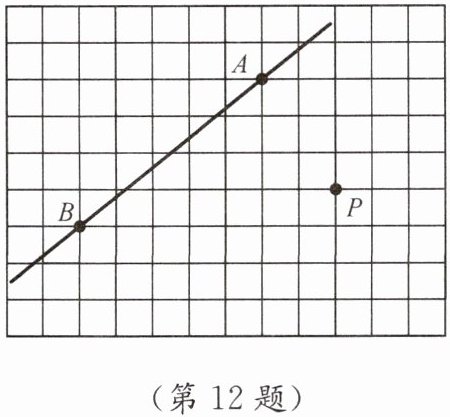
12. 在如图所示的方格纸上过点P画直线AB的平行线;过点P画直线AB的垂线,垂足为H.

答案:
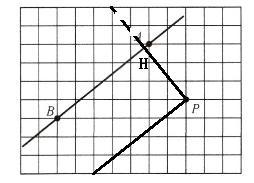

解析:
1. 过点P画直线AB的平行线:
观察直线AB的斜率,确定其方向。
用直尺从点P出发,按照直线AB的斜率方向,画出一条直线,使其与AB平行。
2. 过点P画直线AB的垂线:
直线AB的斜率已知,垂线的斜率是其负倒数。
用直尺从点P出发,画出与直线AB垂直的直线,标记垂足为H。
观察直线AB的斜率,确定其方向。
用直尺从点P出发,按照直线AB的斜率方向,画出一条直线,使其与AB平行。
2. 过点P画直线AB的垂线:
直线AB的斜率已知,垂线的斜率是其负倒数。
用直尺从点P出发,画出与直线AB垂直的直线,标记垂足为H。
13. 如图,将一块三角板的直角顶点放在直尺的一边上.如果∠1= 70°,那么∠2=
20
°.答案:20
解析:
∵直尺两边平行,
∴∠1的同位角等于∠1=70°,
∵三角板直角顶点在直尺上,
∴∠2+70°=90°,
∴∠2=20°.
20
14. 如图,直线AB//CD,直线l分别交AB,CD于点M,N,∠BMN的平分线MF交CD于点F,∠MNF= 40°,则∠DFM=

110
°.
答案:110
解析:
∵AB//CD,∠MNF=40°,
∴∠BMN=∠MNF=40°(两直线平行,内错角相等)。
∵MF平分∠BMN,
∴∠BMF=∠FMN=∠BMN/2=40°/2=20°。
∵AB//CD,
∴∠DFM+∠BMF=180°(两直线平行,同旁内角互补),
∴∠DFM=180°-∠BMF=180°-20°=160°。
160
15. (8分)一个角的余角比它的补角的$\frac{2}{3}$还少40°,求这个角.
答案:解:设这个角为x°
由题$,90-x+40=\frac {2}{3}(180-x)$
解得x=30
∴这个角30°
由题$,90-x+40=\frac {2}{3}(180-x)$
解得x=30
∴这个角30°